《2025年全品学练考九年级数学上册人教版》

操作尝试
如图23-1-3，在硬纸板上，挖一个三角形洞，再另挖一个小洞O作为旋转中心，硬纸板下面放一张白纸。先在纸上描出这个挖掉的三角形图案（△ABC），然后围绕旋转中心转动硬纸板，再描出这个挖掉的三角形（△A'B'C'），移开硬纸板。△A'B'C'是由△ABC绕点O旋转得到的。线段OA与OA'有什么关系？∠AOA'与∠BOB'有什么关系？△ABC与△A'B'C'的形状和大小有什么关系？

答案： 1. 对于线段$OA$与$OA'$的关系：
解：根据旋转的性质，旋转中心到对应点的距离相等。
因为$\triangle A'B'C'$是由$\triangle ABC$绕点$O$旋转得到的，$A$与$A'$是对应点，所以$OA = OA'$。
2. 对于$\angle AOA'$与$\angle BOB'$的关系：
解：根据旋转的性质，对应点与旋转中心所连线段的夹角等于旋转角。
因为$\triangle A'B'C'$是由$\triangle ABC$绕点$O$旋转得到的，$A$与$A'$，$B$与$B'$是对应点，所以$\angle AOA'$和$\angle BOB'$都等于旋转角，即$\angle AOA'=\angle BOB'$。
3. 对于$\triangle ABC$与$\triangle A'B'C'$的形状和大小的关系：
解：根据旋转的性质，旋转前后的图形全等。
因为$\triangle A'B'C'$是由$\triangle ABC$绕点$O$旋转得到的，所以$\triangle ABC\cong\triangle A'B'C'$，即$\triangle ABC$与$\triangle A'B'C'$的形状相同，大小相等。
综上，线段$OA = OA'$；$\angle AOA'=\angle BOB'$；$\triangle ABC$与$\triangle A'B'C'$形状相同，大小相等。

旋转的性质：
（1）对应点到旋转中心的距离相等。
（2）对应点与旋转中心所连线段的夹角等于旋转角。
（3）旋转前、后的图形全等。

答案： [概括新知]
(1)相等
(2)旋转角
(3)全等

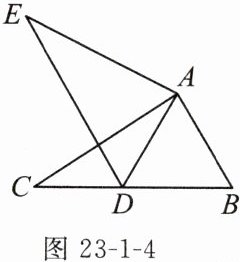
例3（教材补充例题）如图23-1-4，在△ABC中，AB=2，BC=3.6，∠B=60°，将△ABC绕点A顺时针旋转一定的角度后得到△ADE，当点B的对应点D恰好落在BC边上时，CD的长为1.6，旋转角的度数为60°。

答案： 例 3 1.6 60°

变式 如图23-1-5，将△ABC绕点A逆时针旋转到△ADE的位置，旋转角为α（0°＜α＜180°），点B的对应点D恰好落在BC边上。若DE⊥AC，∠CAD=24°，则旋转角α的度数为（C）

A.24°
B.28°
C.48°
D.66°

答案： 变式 C

1. 李明家有一个时钟，某天上午他8点整出门锻炼，回家时发现时针刚好旋转了60°，那么李明回家的时间是（C）
A.9点整
B.9点半
C.10点整
D.10点半

答案： [课堂检测]1. C

2. 如图23-1-6，点A，B，C，D，O都在方格纸的格点上，若△AOB绕点O按逆时针方向旋转到△COD的位置，则旋转的角度为（C）

A.30°
B.45°
C.90°
D.135°

答案： 2. C

3. 如图23-1-7，杠杆绕支点转动撬起重物，杠杆的旋转中心是点 O，旋转角是∠AOA'或∠BOB'。

答案： 3. 点 O ∠AOA'或∠BOB'

4. 如图23-1-8，△A'OB'是由△AOB绕点O按逆时针方向旋转得到的。已知∠AOB=20°，∠A'OB=24°，AB=3，OA=5，则A'B'=3，OA'=5，旋转角等于44°。

答案： 4. 3 5 44

5. 如图23-1-9，将△ABC绕点A逆时针旋转得到△ADE，点C和点E是对应点。若∠CAE=90°，AB=1，则BD的长为$\sqrt{2}$。

答案： 5. $\sqrt{2}$