《2025年全品学练考九年级数学上册人教版》

拓展1 若关于x的方程$x^{k+1}−x+5=0$是一元二次方程，则k=1。

答案： 1

拓展2 若关于x的方程$(k−2)x^{|k|}−8x+6=1$是一元二次方程，则k=-2。

答案： -2

例2(教材典题)将方程3x(x−1)=5(x+2)化成一元二次方程的一般形式，并写出其中的二次项系数、一次项系数和常数项。

答案： 一般形式是$3x^{2}-8x - 10 = 0$，其中二次项系数为 3，一次项系数为-8，常数项为-10

变式一个关于x的一元二次方程，它的二次项系数为3，一次项系数为2，常数项为−6，则这个一元二次方程是$3x^{2}+2x - 6 = 0$。

答案： $3x^{2}+2x - 6 = 0$

一元二次方程的根：使方程左右两边相等的未知数的值就是这个一元二次方程的解，一元二次方程的解也叫做一元二次方程的根。

答案： 相等 根

例3(教材补充例题)下列哪些数是方程x²+3x+2=0的根？
−3，−2，−1，0，1，2，3。

答案： 解: -1，-2 是方程$x^{2}+3x + 2 = 0$的根.

拓展1(2024深圳)一元二次方程x²−4x+a=0的一个根为x=1，则a=3。

答案： 3

拓展2 若a是一元二次方程x²+2x−3=0的一个根，则2a²+4a的值是6。

答案： 6

1. 下列方程中，是一元二次方程的是$ ( B)A. x²+\frac{1}{x}=1B. 2x²−x=1C. 3x³=1D. xy=4$

答案： B

2. 将一元二次方程3x²−2=4x化成一般形式后，二次项系数和一次项系数分别为 (C)
A. 3，−2
B. 3，4
C. 3，−4
D. 3x²，−4x

答案： C

3. 若m是方程x²+4x−5=0的一个根，则m²+4m=5。

答案： 5

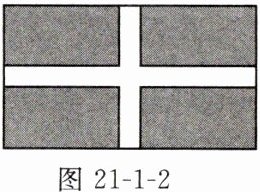
4. 如图21-1-2，学校课外生物小组的试验园地的形状是长35米、宽20米的矩形，为便于管理，要在中间开辟一横一纵共两条等宽的小道，使种植面积为594平方米，则小道的宽为多少米？若设小道的宽为x米，则根据题意列方程为$(35 - x)(20 - x) = 594$，化成一般形式为$x^{2}-55x + 106 = 0$。

答案： $(35 - x)(20 - x) = 594$ $x^{2}-55x + 106 = 0$