《2025年全品学练考九年级数学上册人教版》

操作尝试
剪一个圆形纸片，沿着它的任意一条直径对折，重复做几次，你发现了什么？
推理证明
求证：圆是轴对称图形，任何一条直径所在直线都是圆的对称轴。

答案：
[操作尝试]
解:沿着圆的任意一条直径对折，直径两侧的部分总能重合.
[推理证明]
证明:如图，设 $ CD $ 是 $ \odot O $ 的任意一条直径， $ A $ 为 $ \odot O $ 上点 $ C $， $ D $ 以外的任意一点。过点 $ A $ 作 $ AA' \perp CD $，交 $ \odot O $ 于点 $ A' $，垂足为 $ M $，连接 $ OA $， $ OA' $。
在 $ \triangle OAA' $ 中， $ \because OA = OA' $，
$ \therefore \triangle OAA' $ 是等腰三角形。
又 $ AA' \perp CD $， $ \therefore AM = MA' $。
即 $ CD $ 是 $ AA' $ 的垂直平分线。这就是说，对于圆上任意一点 $ A $，在圆上都有关于直线 $ CD $ 的对称点 $ A' $，因此 $ \odot O $ 关于直线 $ CD $ 对称。
即圆是轴对称图形，任何一条直径所在直线都是圆的对称轴。

圆的轴对称性：
(1)圆是轴对称图形，任何一条直径所在直线都是圆的对称轴。
(2)圆有无数条对称轴。

答案： （1）轴对称 对称轴 （2）无数

例1(教材补充例题)下列说法正确的是 (C)
A.每一条直径都是圆的对称轴
B.圆的对称轴是唯一的
C.圆的对称轴一定经过圆心
D.圆的对称轴是经过圆内任意一点的直线

答案： 例 1 C

1. 如图24-1-6所示，从上面[推理证明]的解答过程可知，如果⊙O的直径CD垂直于弦AA'，垂足为M，那么点A和点A'是对称点，图中除OC=OD外，还有哪些相等的线段和劣弧？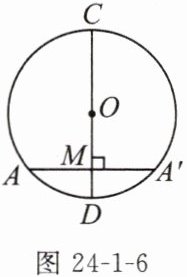

答案： [问题情境]
1. $ AM = A'M $， $ \overset{\frown}{AC} = \overset{\frown}{A'C} $， $ \overset{\frown}{AD} = \overset{\frown}{A'D} $

2. (1)如图24-1-7，若直径CD与弦AA'相交于点M，且CD平分AA'，弦AA'不过圆心O，则CD垂直于AA'吗？图中还有哪些劣弧相等？
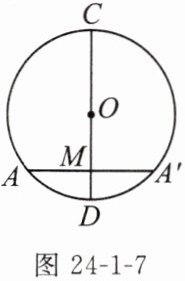
(2)在(1)中，若弦AA'过圆心O，上面得到的结论还成立吗？

答案： 2. 解：（1）连接 $ OA $， $ OA' $。
$ \because CD $ 平分弦 $ AA' $， $ \therefore AM = A'M $。
又 $ \because OA = OA' $， $ \therefore CD \perp AA' $，
$ \therefore $ 点 $ A $ 与点 $ A' $ 关于直线 $ CD $ 对称， $ \overset{\frown}{AC} $ 和 $ \overset{\frown}{A'C} $ 对称， $ \overset{\frown}{AD} $ 和 $ \overset{\frown}{A'D} $ 对称，
$ \therefore \overset{\frown}{AC} = \overset{\frown}{A'C} $， $ \overset{\frown}{AD} = \overset{\frown}{A'D} $。
（2）不一定成立。

垂径定理及其推论：

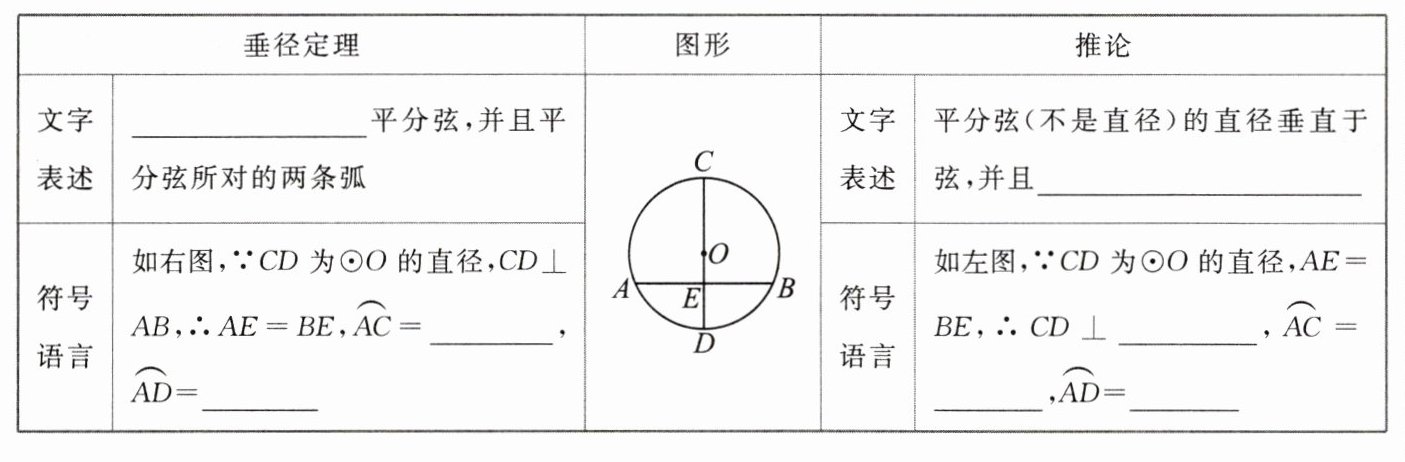
答案： 垂直于弦的直径 $ \overset{\frown}{BC} $ $ \overset{\frown}{BD} $ 平分弦所对的两条弧 $ AB $ $ \overset{\frown}{BC} $ $ \overset{\frown}{BD} $