《2025年全品学练考九年级数学上册人教版》

1. (2024成都)在平面直角坐标系xOy中，点P(1,-4)关于原点对称的点的坐标是 (B)
A. (-1,-4)
B. (-1,4)
C. (1,4)
D. (1,-4)

答案： B

2. 点P(a,-3)关于原点对称的点是P'(4,c)，则a-c的值是 (A)
A. -7
B. -1
C. -5
D. 5

答案： A

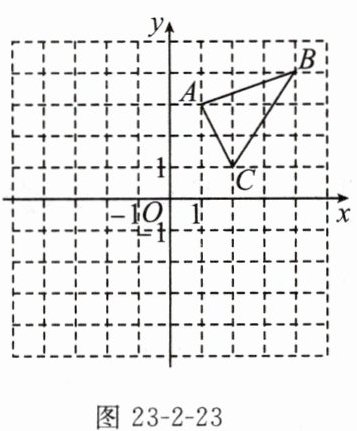
3. 如图23-2-23，在平面直角坐标系中，△ABC的三个顶点分别是A(1,3)，B(4,4)，C(2,1)。
(1)把△ABC向左平移4个单位长度后得到△A₁B₁C₁，请画出平移后的△A₁B₁C₁；
(2)把△ABC绕原点O旋转180°后得到△A₂B₂C₂，请画出旋转后的△A₂B₂C₂；
(3)观察图形可知，△A₁B₁C₁与△A₂B₂C₂关于点(-2，0)中心对称。

答案： 1. （1）
已知$A(1,3)$，$B(4,4)$，$C(2,1)$，根据平移规律“左减右加，上加下减”，向左平移$4$个单位长度，横坐标减$4$，纵坐标不变。
则$A_1(1 - 4,3)$，即$A_1(-3,3)$；$B_1(4 - 4,4)$，即$B_1(0,4)$；$C_1(2 - 4,1)$，即$C_1(-2,1)$。然后根据$A_1$、$B_1$、$C_1$的坐标画出$\triangle A_1B_1C_1$。
2. （2）
已知$A(1,3)$，$B(4,4)$，$C(2,1)$，根据绕原点$O$旋转$180^{\circ}$的坐标变化规律“$(x,y)$旋转$180^{\circ}$后变为$(-x,-y)$”。
则$A_2(-1,-3)$；$B_2(-4,-4)$；$C_2(-2,-1)$。然后根据$A_2$、$B_2$、$C_2$的坐标画出$\triangle A_2B_2C_2$。
3. （3）
设$\triangle A_1B_1C_1$与$\triangle A_2B_2C_2$关于点$(a,b)$中心对称，根据中心对称的性质，若点$(x_1,y_1)$与$(x_2,y_2)$关于点$(a,b)$中心对称，则$a=\frac{x_1 + x_2}{2}$，$b=\frac{y_1 + y_2}{2}$。
取$A_1(-3,3)$与$A_2(-1,-3)$，则$a=\frac{-3+( - 1)}{2}=\frac{-4}{2}=-2$，$b=\frac{3+( - 3)}{2}=0$。
也可验证$B_1(0,4)$与$B_2(-4,-4)$：$a=\frac{0+( - 4)}{2}=-2$，$b=\frac{4+( - 4)}{2}=0$；$C_1(-2,1)$与$C_2(-2,-1)$：$a=\frac{-2+( - 2)}{2}=-2$，$b=\frac{1+( - 1)}{2}=0$。
故答案依次为：$-2$；$0$。

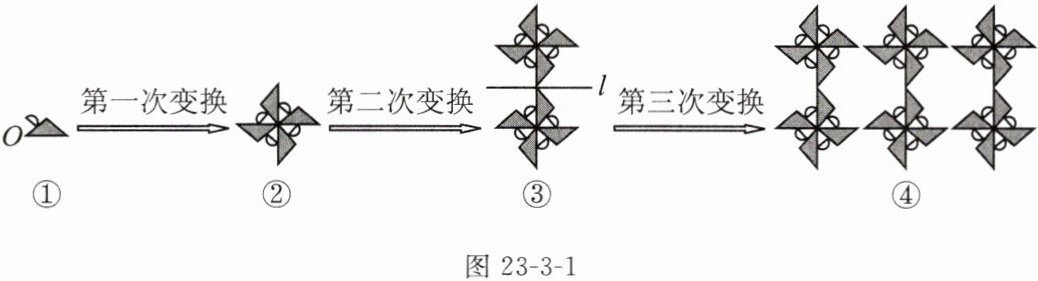
观察图23-3-1①~④的变换过程,说出每一次的变换方式.

答案： 第一次变换是绕点$O$旋转$90^{\circ}$（或旋转）；第二次变换是关于直线$l$作轴对称（或轴对称）；第三次变换是平移（或连续平移）。

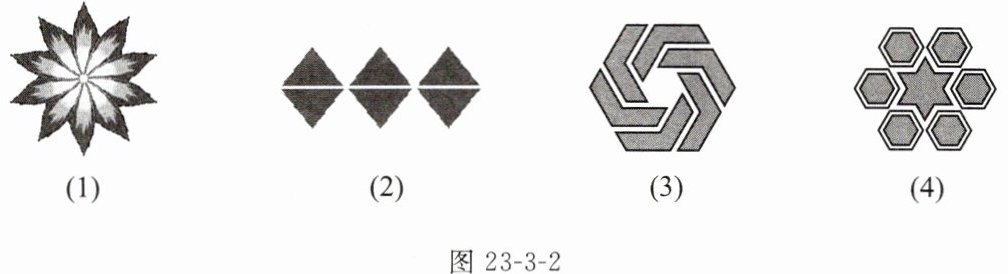
例1(教材补充例题)分析下列图案的形成过程.

答案：
解:图
(1)是由基本图形 旋转九次后得到的;图
(2)是由基本图形 平移两次后得到的;图
(3)是由基本图形 旋转五次后得到的;图
(4)是由基本图形旋转五次后得到的.图案的形成过程不唯一，还可以有其他的形成过程，如图
(1)
(4)还可以分别由图形 通过轴对称变换得到