《2025年全品学练考九年级数学上册人教版》

填上适当的数或式，使下列各等式成立。
①$x^{2}+2x+$1$=(x+$1$)^{2}$；②$x^{2}-4x+$4$=(x-$2$)^{2}$；
③$x^{2}+$12x$+36=(x+6)^{2}$； ④$x^{2}+10x+$25$=(x+$5$)^{2}$。

答案： ①1 1 ②4 2 ③12x ④25 5

归纳总结
$x^{2}+px+$($\frac{p}{2}$)$^{2}=(x+$$\frac{p}{2}$$)^{2}$。

答案： $\frac{p}{2}$ $\frac{p}{2}$

怎样解方程$x^{2}+6x+4=0$？
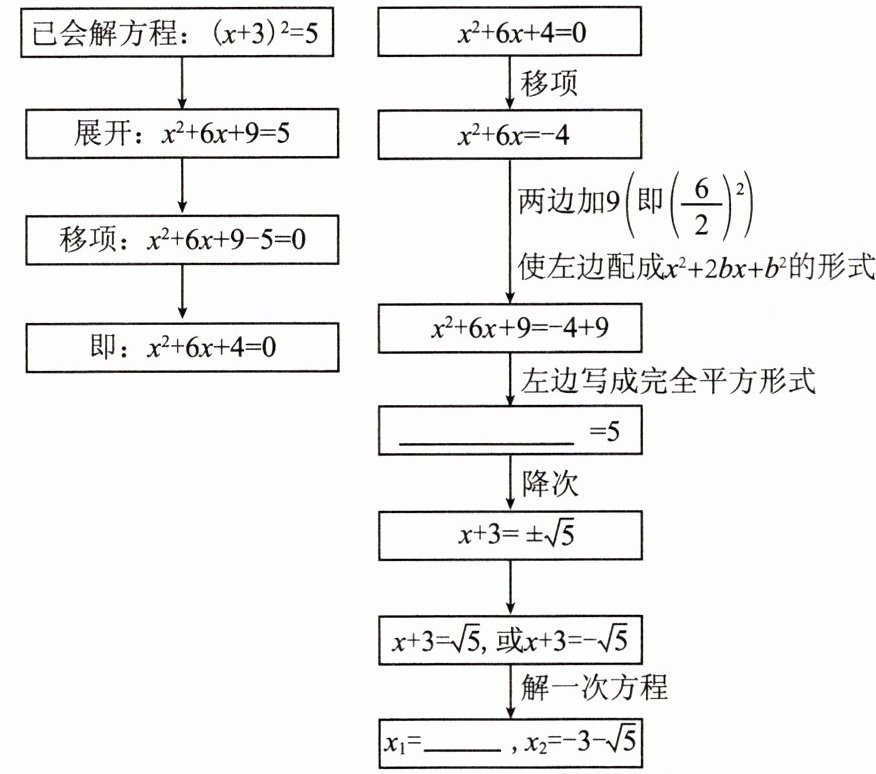
请看下面框图左边的提示，然后把左边从下向上尝试得到右边部分，并进行适当的填空：

答案： $(x + 3)^2$ $-3 + \sqrt{5}$

1. 配方法：将一元二次方程$ax^{2}+bx+c=0(a≠0)$经过配方得到$(x+h)^{2}=k$(h，k均为常数)，然后再用直接开平方法来解，这种方法叫做配方法，可以看出，配方是为了降次，把一个一元二次方程转化成两个一元一次方程来解。

答案： 1. 配方法 降次 一元一次方程