《2025年全品学练考九年级数学上册人教版》

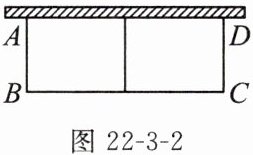
变式1 如图22-3-2,有长为30m的篱笆,一面利用墙(墙的长度为10m),围成中间隔有一道篱笆(平行于AB)的矩形菜园.设菜园的一边AB的长为xm,矩形ABCD的面积为$ym^{2}$.
(1)求y与x之间的函数解析式;
(2)当x为何值时,y的值最大? 求出y的最大值.

答案：
(1)$y = -3x^2 + 30x(\frac{20}{3} \leq x ＜ 10)$
(2)当$x = \frac{20}{3}$时，y的值最大，最大值为$\frac{200}{3}$

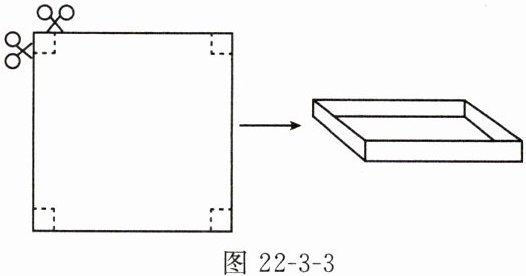
变式2 某校九年级学生在数学社团课上进行纸盒设计,利用一个边长为30cm的正方形硬纸板,在正方形纸板的四角各剪掉一个同样大小的小正方形,将剩余部分折成一个无盖纸盒.
(1)若无盖纸盒的底面积为$484cm^{2}$,则剪掉的小正方形的边长为多少?
(2)折成的无盖纸盒的侧面积是否有最大值? 如果有,求出这个最大值和此时剪掉的小正方形的边长;如果没有,说明理由.

答案：
(1)4cm
(2)折成的无盖纸盒的侧面积有最大值，最大值为450$cm^2$，此时剪掉的小正方形的边长为$\frac{15}{2}$cm

1. 已知直角三角形两条直角边的和为18,则当这个直角三角形的面积最大时,两条直角边分别为(B)
A. 8,10
B. 9,9
C. 7,11
D. 6,12

答案： B

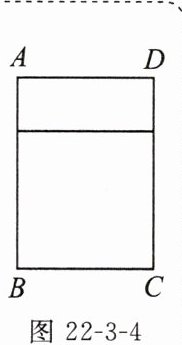
2. 常青钢窗厂要利用12米长的钢材制成如图22-3-4所示的矩形窗框,窗框的长与宽分别为多少时,此窗框的透光面积最大? 最大面积是多少?

答案： 窗框的长AB为3米，宽AD为2米时，窗框的透光面积最大，最大面积是6平方米

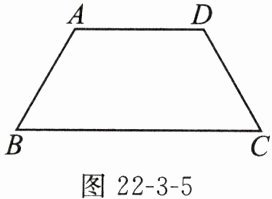
3. 如图22-3-5,等腰梯形ABCD的周长为4cm,$∠B = ∠C = 60^{\circ}$,当梯形的腰长为多少时,梯形的面积最大? 最大面积是多少?

答案： 当梯形的腰长为1cm时，梯形的面积最大，最大面积是$\frac{\sqrt{3}}{2}cm^2$