《2025年全品学练考九年级数学上册人教版》

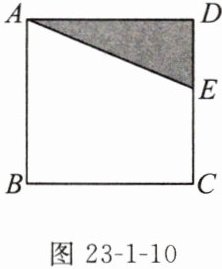
如图23-1-10，E是正方形ABCD中CD边上任意一点，以点A为中心，把△ADE顺时针旋转90°，画出旋转后的图形.请你尽可能多地说出你的画法.

答案： 1. 方法一：
延长$CB$到$F$，使$BF = DE$，连接$AF$，则$\triangle ABF$就是$\triangle ADE$绕点$A$顺时针旋转$90^{\circ}$后的图形。
理由：
因为四边形$ABCD$是正方形，所以$AD = AB$，$\angle D=\angle ABC = 90^{\circ}$，$\angle ABF = 180^{\circ}-\angle ABC=90^{\circ}$。
在$\triangle ADE$和$\triangle ABF$中，$\left\{\begin{array}{l}AD = AB\\\angle D=\angle ABF\\DE = BF\end{array}\right.$，根据$SAS$（边角边）定理$\triangle ADE\cong\triangle ABF$。
又因为$\angle DAB = 90^{\circ}$，所以$\triangle ABF$是$\triangle ADE$绕点$A$顺时针旋转$90^{\circ}$得到的。
2. 方法二：
以点$A$为圆心，$AE$长为半径画弧，交$CB$的延长线于点$F$，连接$AF$，则$\triangle ABF$就是$\triangle ADE$绕点$A$顺时针旋转$90^{\circ}$后的图形。
理由：
因为四边形$ABCD$是正方形，所以$AD = AB$，$\angle DAB = 90^{\circ}$。
由旋转的性质可知，旋转前后对应点到旋转中心的距离相等，$AE = AF$，$\angle DAE=\angle BAF$（因为$\angle DAB=\angle DAE + \angle EAB=\angle BAF+\angle EAB = 90^{\circ}$），且$AD = AB$，所以$\triangle ADE$绕点$A$顺时针旋转$90^{\circ}$后与$\triangle ABF$重合。
综上，画法有：（1）延长$CB$到$F$，使$BF = DE$，连接$AF$；（2）以点$A$为圆心，$AE$长为半径画弧，交$CB$的延长线于点$F$，连接$AF$。

例 (教材补充例题)如图23-1-11，△ABC绕点O旋转后得到△A'B'C'，顶点A的对应点为A'.
(1)试确定旋转后的三角形；
(2)指出旋转角.

答案： 1. （1）
解：连接$OA$，$OA'$，作$\angle BOB'=\angle AOA'$，且$OB' = OB$，作$\angle COC'=\angle AOA'$，且$OC' = OC$，连接$A'B'$，$B'C'$，$C'A'$，则$\triangle A'B'C'$就是$\triangle ABC$绕点$O$旋转后的三角形。
2. （2）
解：旋转角为$\angle AOA'$，$\angle BOB'$，$\angle COC'$。

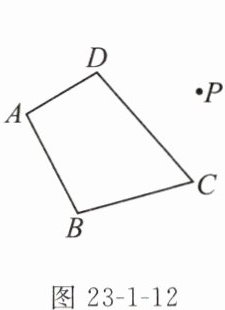
变式1 如图23-1-12，画出四边形ABCD绕点P顺时针旋转60°后的图形.

答案： 1. 首先，连接$PA$、$PB$、$PC$、$PD$：
以$PA$为例，根据旋转的性质，将$\overrightarrow{PA}$绕点$P$顺时针旋转$60^{\circ}$，得到$\overrightarrow{PA'}$，使得$PA = PA'$，$\angle APA'=60^{\circ}$。
同样的方法，将$\overrightarrow{PB}$绕点$P$顺时针旋转$60^{\circ}$，得到$\overrightarrow{PB'}$，满足$PB = PB'$，$\angle BPB' = 60^{\circ}$。
将$\overrightarrow{PC}$绕点$P$顺时针旋转$60^{\circ}$，得到$\overrightarrow{PC'}$，满足$PC = PC'$，$\angle CPC'=60^{\circ}$。
将$\overrightarrow{PD}$绕点$P$顺时针旋转$60^{\circ}$，得到$\overrightarrow{PD'}$，满足$PD = PD'$，$\angle DPD'=60^{\circ}$。
2. 然后，连接$A'B'$、$B'C'$、$C'D'$、$D'A'$：
四边形$A'B'C'D'$就是四边形$ABCD$绕点$P$顺时针旋转$60^{\circ}$后的图形。
（具体画图过程需借助量角器和直尺完成，先确定旋转中心$P$，再根据旋转角和旋转方向确定各顶点的对应点，最后顺次连接对应点）。

变式2 如图23-1-13，画出四边形ABCD绕点O按顺时针方向旋转120°后得到的图形.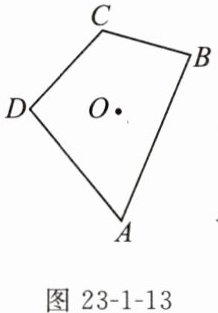

答案： 1. 首先，连接$OA$、$OB$、$OC$、$OD$：
以$OA$为例，将$OA$绕点$O$顺时针旋转$120^{\circ}$，得到$OA'$，使$\angle AOA' = 120^{\circ}$，且$OA'=OA$。
设$OA$与$x$轴正半轴夹角为$\alpha$，根据旋转的性质，$OA'$与$x$轴正半轴夹角为$\alpha - 120^{\circ}$（若$\alpha\geqslant120^{\circ}$），利用量角器和圆规来确定$A'$的位置。
同理，对于$OB$，绕点$O$顺时针旋转$120^{\circ}$得到$OB'$，使$\angle BOB' = 120^{\circ}$，且$OB' = OB$；对于$OC$，绕点$O$顺时针旋转$120^{\circ}$得到$OC'$，使$\angle COC' = 120^{\circ}$，且$OC' = OC$；对于$OD$，绕点$O$顺时针旋转$120^{\circ}$得到$OD'$，使$\angle DOD' = 120^{\circ}$，且$OD' = OD$。
2. 然后，连接$A'B'$、$B'C'$、$C'D'$、$D'A'$：
四边形$A'B'C'D'$就是四边形$ABCD$绕点$O$按顺时针方向旋转$120^{\circ}$后得到的图形。
具体画图步骤：
步骤一：用圆规分别以$O$为圆心，$OA$、$OB$、$OC$、$OD$长为半径画弧。
步骤二：用量角器分别以$OA$、$OB$、$OC$、$OD$为一边，绕$O$点顺时针作$120^{\circ}$的角，角的另一边与相应弧的交点分别为$A'$、$B'$、$C'$、$D'$。
步骤三：依次连接$A'B'$、$B'C'$、$C'D'$、$D'A'$。
（由于是画图题，这里主要阐述方法，实际画图需借助工具完成）

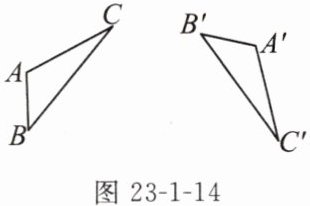
如图23-1-14，△A'B'C'是由△ABC旋转得到的，你能找出旋转中心点O吗？(要求尺规作图)

答案： 1. 首先，连接$AA'$：
用尺规作线段$AA'$的垂直平分线$l_1$。根据垂直平分线的性质，线段垂直平分线上的点到线段两端点的距离相等，旋转中心$O$在$AA'$的垂直平分线上（因为旋转中心到对应点$A$与$A'$的距离相等）。
2. 然后，连接$BB'$：
用尺规作线段$BB'$的垂直平分线$l_2$。同理，旋转中心$O$在$BB'$的垂直平分线上（因为旋转中心到对应点$B$与$B'$的距离相等）。
3. 最后：
两条垂直平分线$l_1$与$l_2$的交点$O$就是旋转中心。
具体尺规作图步骤：
作线段$AA'$垂直平分线：
分别以$A$、$A'$为圆心，大于$\frac{1}{2}AA'$的长为半径画弧（两弧半径相等），两弧分别相交于两点。
过这两点作直线$l_1$。
作线段$BB'$垂直平分线：
分别以$B$、$B'$为圆心，大于$\frac{1}{2}BB'$的长为半径画弧（两弧半径相等），两弧分别相交于两点。
过这两点作直线$l_2$。
$l_1$与$l_2$的交点$O$即为所求的旋转中心。

旋转中心的确定
旋转中心是两对对应点所连线段的垂直平分线的交点.

答案： 垂直平分线