第79页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
11.(2024·合肥肥东县模拟)某年级为了解某次数学考试情况,随机抽取了部分学生的成绩(得分均为整数,满分为150分),并将成绩分组如下:第一组(75≤x<90)、第二组(90≤x<105)、第三组(105≤x<120)、第四组(120≤x<135)、第五组(135≤x≤150). 并将成绩绘制成如图所示的频数分布直方图和扇形统计图(不完整):
学生数学考试成绩
频数分布直方图 各组学生人数所占百分比
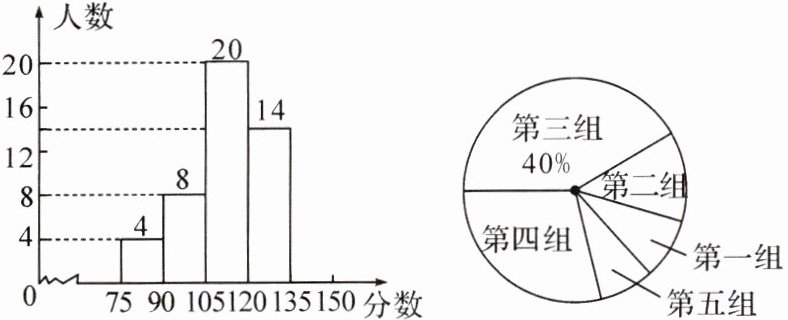
根据图中信息,回答下列问题:
(1)本次调查随机抽取了______名学生,并将频数分布直方图补充完整;
(2)若该年级共有1 500名考生,估计成绩在120分以上(含120分)学生有______名;
(3)如果第一组(75≤x<90)中只有一名是女生,第五组(135≤x≤150)中只有一名是男生,现从第一组、第五组分别随机选出一名同学谈答题感想,试求所选两名学生刚好是一名女生和一名男生的概率.
学生数学考试成绩
频数分布直方图 各组学生人数所占百分比

根据图中信息,回答下列问题:
(1)本次调查随机抽取了______名学生,并将频数分布直方图补充完整;
(2)若该年级共有1 500名考生,估计成绩在120分以上(含120分)学生有______名;
(3)如果第一组(75≤x<90)中只有一名是女生,第五组(135≤x≤150)中只有一名是男生,现从第一组、第五组分别随机选出一名同学谈答题感想,试求所选两名学生刚好是一名女生和一名男生的概率.
答案:
解:
(1)50 本次调查随机抽取的学生人数为20÷40% = 50(人),则第五组(135≤$x$≤150)的学生人数为50 - 4 - 8 - 20 - 14 = 4(人).补全频数分布直方图略.
(2)540
(3)第一组(75≤$x$<90)中只有一名是女生,则男生有3名,第五组(135≤$x$≤150)中只有一名是男生,则女生有3名.画树状图如下: 共有16种等可能的结果,其中所选两名学生刚好是一名女生和一名男生的结果有10种,
共有16种等可能的结果,其中所选两名学生刚好是一名女生和一名男生的结果有10种,
∴所选两名学生刚好是一名女生和一名男生的概率为$\frac{10}{16}=\frac{5}{8}$.
解:
(1)50 本次调查随机抽取的学生人数为20÷40% = 50(人),则第五组(135≤$x$≤150)的学生人数为50 - 4 - 8 - 20 - 14 = 4(人).补全频数分布直方图略.
(2)540
(3)第一组(75≤$x$<90)中只有一名是女生,则男生有3名,第五组(135≤$x$≤150)中只有一名是男生,则女生有3名.画树状图如下:
 共有16种等可能的结果,其中所选两名学生刚好是一名女生和一名男生的结果有10种,
共有16种等可能的结果,其中所选两名学生刚好是一名女生和一名男生的结果有10种,∴所选两名学生刚好是一名女生和一名男生的概率为$\frac{10}{16}=\frac{5}{8}$.
12.(2024·宿州灵璧县期末)某射击运动员在同一条件下的射击结果如下表:
|射击总次数n|10|20|50|100|200|500|1 000|
|----|----|----|----|----|----|----|----|
|击中靶心的次数m|9|16|41|88|168|429|861|
|击中靶心的频率|0.90|0.8|0.82|0.88|0.84|0.858|0.861|
根据频率的稳定性,估计这名运动员射击一次时击中靶心的概率是________(结果保留两位小数).
|射击总次数n|10|20|50|100|200|500|1 000|
|----|----|----|----|----|----|----|----|
|击中靶心的次数m|9|16|41|88|168|429|861|
|击中靶心的频率|0.90|0.8|0.82|0.88|0.84|0.858|0.861|
根据频率的稳定性,估计这名运动员射击一次时击中靶心的概率是________(结果保留两位小数).
答案:
0.86
13.(2024·芜湖无为市月考)二维码在日常生活中被广泛应用,某数学兴趣小组对其开展数学活动. 如图,在边长为2 cm的正方形区域内利用计算机软件进行随机掷点模拟试验. 经过大量重复试验发现,点落在黑色部分的频率稳定在0.7左右,据此可以估计这个正方形区域内黑色部分的面积约为__________.
答案:
2.8 $cm^{2}$
14.【数学文化】汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝. 如图,四个直角三角形都是全等的,它们的两直角边之比均为3∶4. 现随机向该图形内掷一枚小针,则针尖落在阴影区域的概率为________.
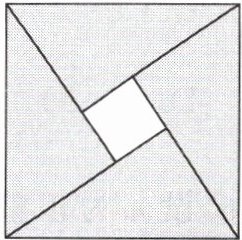

答案:
$\frac{24}{25}$
查看更多完整答案,请扫码查看


