《2025年名校课堂九年级数学下册沪科版安徽专版》

10. 如图，A，B，C，D，E，F是⊙O的六等分点，则∠ACB等于 （ ）

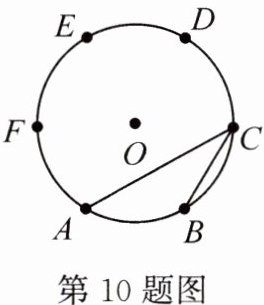
A. 60°
B. 45°
C. 30°
D. 22.5°

答案： C

11. 若正三角形、正方形、正六边形的周长相等，它们的面积分别为S₁，S₂，S₃，则下列关系成立的是 （ ）
A. S₁ = S₂ = S₃
B. S₁＞S₂＞S₃
C. S₁＜S₂＜S₃
D. S₂＞S₃＞S₁

答案： C

12.（2024·宣城模拟）如图，将圆周六等分，B，D是其中两个等分点，点A，C分别在优弧$\overset{\frown}{BD}$和劣弧$\overset{\frown}{BD}$上，则∠BAD∶∠BCD的值是____.

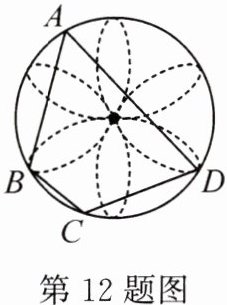
答案： $\frac{1}{2}$

13. 如图，在正五边形ABCDE中，点F，G分别是BC，CD的中点，AF，BG相交于点H.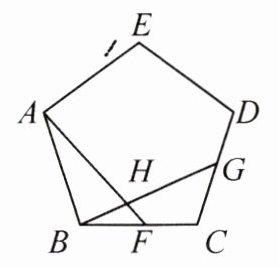
（1）求证：△ABF≌△BCG；
（2）求∠AHG的度数.

答案： 解：（1）证明：
∵五边形ABCDE是正五边形，
∴AB = BC = CD，∠ABF = ∠BCG.
∵F，G分别是BC，CD的中点，
∴BF = CG. 在△ABF和△BCG中，$\begin{cases}AB = BC,\\\angle ABF = \angle BCG,\\BF = CG,\end{cases}$
∴△ABF≌△BCG（SAS）. （2）
∵△ABF≌△BCG，
∴∠GBC = ∠FAB.
∴∠AHG = ∠FAB + ∠ABH = ∠GBC + ∠ABH = ∠ABC.
∵正五边形的内角为108°，
∴∠AHG = 108°.

14. 已知正方形ABCD内接于⊙O，点P是$\overset{\frown}{AD}$上一点.
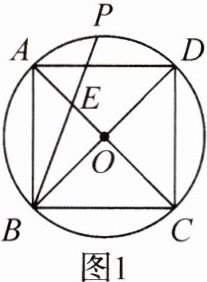
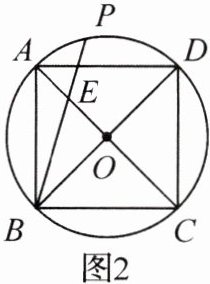
（1）如图1，若点P是$\overset{\frown}{AD}$的中点，求证：CE = CD；
（2）如图2，若PE = OE，求$\frac{AE}{EC}$的值.

答案： 解：（1）证明：连接DE，
∵四边形ABCD是正方形，
∴∠ABD = ∠DCE = ∠CDO = 45°，AC⊥BD，OB = OD = OC.
∴EB = ED.
∴∠PBD = ∠EDB.
∵点P是$\overset{\frown}{AD}$的中点，
∴∠EDB = ∠PBD = $\frac{1}{2}$∠ABD = 22.5°.
∴∠EDC = ∠CDO + ∠EDB = 45° + 22.5° = 67.5°.
∴∠CED = 180° - ∠DCE - ∠CDE = 180° - 45° - 67.5° = 67.5°.
∴∠CED = ∠EDC.
∴CE = CD. （2）连接DE，DP，
∵四边形ABCD是正方形，
∴∠BAD = ∠EOD = 90°，OA = OD.
∴∠P = ∠BAD = 90°.
∵PE = OE，DE = DE，
∴Rt△PDE≌Rt△ODE（HL）.
∴∠PDE = ∠ODE. 由（1）知，∠PBD = ∠ODE，
∴∠PBD = ∠ODE = ∠PDE.
∵∠PBD + ∠ODE + ∠PDE = 90°，
∴∠ODE = 30°.
∴tan∠ODE = tan30° = $\frac{OE}{OD}$ = $\frac{\sqrt{3}}{3}$.
∴OD = OA = $\sqrt{3}$OE.
∴AE = OA - OE = ($\sqrt{3}$ - 1)OE，EC = OE + OC = ($\sqrt{3}$ + 1)OE.
∴$\frac{AE}{EC}$ = $\frac{\sqrt{3}-1}{\sqrt{3}+1}$ = 2 - $\sqrt{3}$.