《2025年名校课堂九年级数学下册沪科版安徽专版》

9. （教材P43例题变式）如图，$\triangle ABC$是圆的内接三角形，点$P$是$\triangle ABC$的内心，$\angle A = 50^{\circ}$，则$\angle BPC$的度数为______.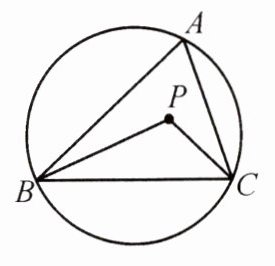

答案： 115°

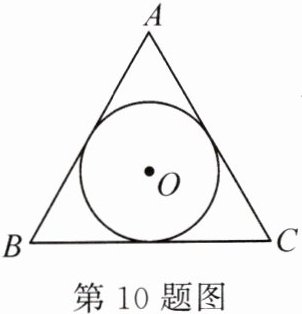
10. 如图，$\odot O$是等边三角形$ABC$的内切圆. 若$AB = 4$，则$\odot O$的半径是 （ ）

A. $\frac{\sqrt{3}}{2}$
B. $1$
C. $\frac{2\sqrt{3}}{3}$
D. $2$

答案： C

11. 已知一个三角形的三边长分别为$5$，$7$，$8$，则其内切圆的半径为______.

答案： $\sqrt{3}$

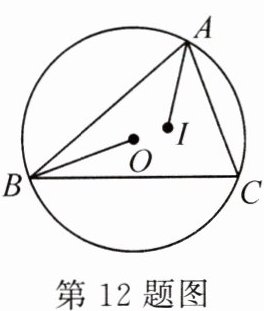
12. （2023·蚌埠期末）如图，点$O$是$\triangle ABC$外接圆的圆心，点$I$是$\triangle ABC$的内心，连接$OB$，$IA$. 若$\angle CAI = 35^{\circ}$，则$\angle OBC$的度数为______.

答案： 20°

13. 如图所示，在平面直角坐标系中，$\odot I$与$x$轴、$y$轴、直线$AB$分别相切于点$D$，$E$，$C$，点$I$的坐标为$(-1,-1)$，点$B$的坐标为$(0,-4)$，求直线$AB$的表达式.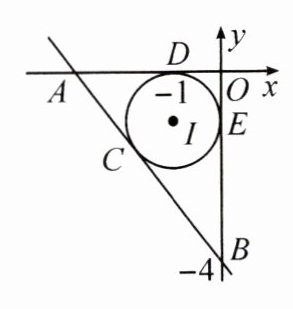

答案： 解：因为⊙I 与 x 轴、y 轴、直线 AB 分别相切于点 D，E，C，所以 AD = AC，BC = BE，OD = OE。因为点 I 的坐标为(-1，-1)，点 B 的坐标为(0，-4)，所以 OD = OE = 1，OB = 4，BE = BC = 3。设 AC = AD = x，则 OA = x + 1，AB = x + 3。因为 OA² + OB² = AB²，所以(x + 1)² + 4² = (x + 3)²，解得 x = 2。所以 A(-3，0)。设直线 AB 的表达式为 y = kx + b，所以$\begin{cases}b = -4\\-3k + b = 0\end{cases}$，解得$\begin{cases}k = -\frac{4}{3}\\b = -4\end{cases}$，所以直线 AB 的表达式为 y = -$\frac{4}{3}$x - 4。

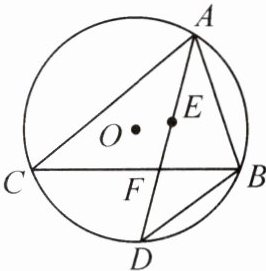
14. （2023·芜湖一模）如图，点$E$是$\triangle ABC$的内心，$AE$的延长线和$\triangle ABC$的外接圆$\odot O$相交于点$D$，与弦$BC$相交于点$F$.
(1) 求证：$DB = DE$；
(2) 若$DF = 3$，$AF = 5$，求$AE$的长.

答案： 解：
(1)证明：连接 BE。因为点 E 是△ABC 的内心，所以∠ABE = ∠CBE，∠BAD = ∠CAD。因为∠CAD = ∠DBC，所以∠BAD = ∠DBC。所以∠DBE = ∠DBC + ∠EBC = ∠ABE + ∠BAD = ∠DEB。所以 DE = DB。
(2)因为∠DBC = ∠DAB，∠D = ∠D，所以△DBF∽△DAB。所以$\frac{DB}{AD}$ = $\frac{DF}{DB}$。所以 DB² = AD·DF。因为 DF = 3，AF = 5，所以 AD = DF + AF = 8。所以 DB² = 8×3 = 24。所以 DB = 2$\sqrt{6}$。所以 DE = DB = 2$\sqrt{6}$。所以 AE = AD - DE = 8 - 2$\sqrt{6}$。

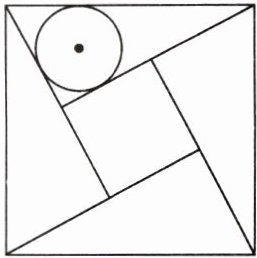
15. 我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形（如图所示）. 若直角三角形的内切圆半径为$3$，小正方形的面积为$49$，则大正方形的面积为______.

答案： 289