《2025年名校课堂九年级数学下册沪科版安徽专版》

10. 在△ABC 中，AC＝BC＝2√2，AB＝4，则△ABC 的内切圆半径为__________.

答案： $2\sqrt{2}-2$

11.（2023·安徽二模）如图，AB，AC 是⊙O 的切线，B，C 为切点，OD//AC 交BC 于点 D. 若∠A＝40°，则∠BOD 的度数是 （ ）

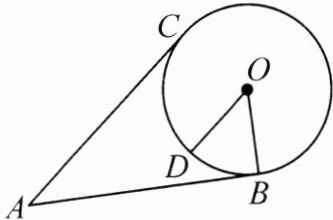
A. 40°
B. 50°
C. 55°
D. 60°

答案： B

12.（2022·安徽）已知 AB 为⊙O 的直径，C 为⊙O 上一点，D 为 BA 的延长线上一点，连接 CD.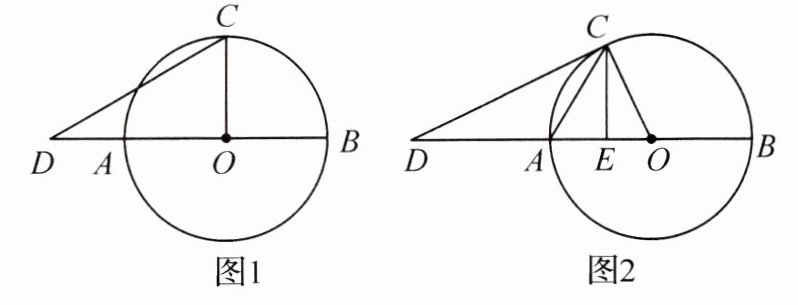
（1）如图 1，若 CO⊥AB，∠D＝30°，OA＝1，求 AD 的长；
（2）如图 2，若 DC 与⊙O 相切，E 为 OA 上一点，且∠ACD＝∠ACE. 求证：CE⊥AB.

答案： 解：
(1)
∵ $OA = OC = 1$，$CO\perp AB$，$\angle D = 30^{\circ}$，
∴ $OD=\sqrt{3}OC=\sqrt{3}$.
∴ $AD = OD - OA=\sqrt{3}-1$.
(2)证明：
∵ $DC$与$\odot O$相切，
∴ $OC\perp CD$，即$\angle ACD+\angle OCA = 90^{\circ}$.
∵ $OA = OC$，
∴ $\angle OCA=\angle OAC$.
∵ $\angle ACD=\angle ACE$，
∴ $\angle OAC+\angle ACE = 90^{\circ}$.
∴ $\angle AEC = 90^{\circ}$，即 $CE\perp AB$.

13.（2022·安徽二模）如图，在正五边形 ABCDE 中，分别以点 C，D 为圆心，边 CD 长为半径画弧，两弧相交于点 F，连接 BF，则∠ABF 的度数为______.

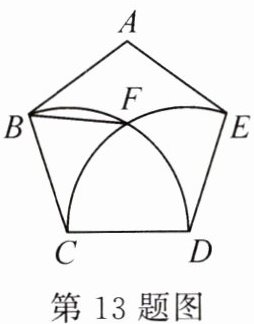
答案： 42°

14.（2023·合肥蜀山区二模）如图，用一个圆心角为θ的扇形纸片围成一个底面半径为 2，侧面积为 8π的圆锥，则该扇形的圆心角θ的大小为 （ ）

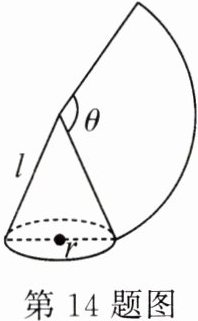
A. 90°
B. 120°
C. 150°
D. 180°

答案： D

15.（2024·合肥 45 中模拟）如图，已知 AB 是⊙O 的弦，C 为⊙O 上的一点，OC⊥AB 于点 D. 若⊙O 的半径为 3，∠ABC＝25°，则BC⌢的长为 （ ）


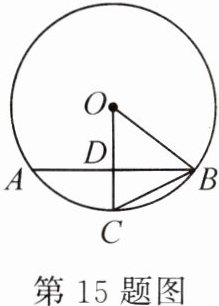
A. 2/3π
B. 5/3π
C. 5/6π
D. 5/12π

答案： C

16.（2024·淮北模拟）如图，将扇形 AOB 翻折，使点 A 与圆心 O 重合，展开后折痕所在直线 l 与AB⌢交于点 C，连接 AC. 若 OA＝2，则图中阴影部分的面积是__________.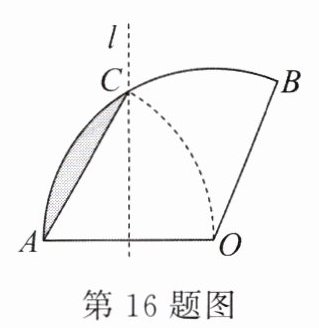

答案： $\frac{2\pi}{3}-\sqrt{3}$

17.《几何原本》中的几何代数法（以几何方法研究代数问题）成为了后世数学家处理问题的重要依据，通过这一原理，很多代数公理或定理都能够通过图形实现证明，也称之为无字证明. 如图，在 AB 上取一点 C，使得 AC＝a，BC＝b，过点 C 作 CD⊥AB 交半圆 O 于点 D，连接 OD. 作 CE⊥OD 于点 E. 则下列不等式可以表示 CD≥DE 的是 （ ）

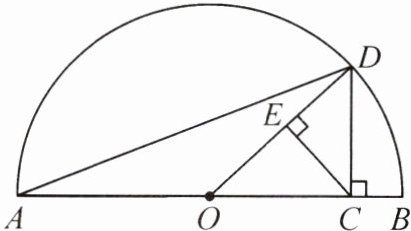
A. √ab≥2ab/(a + b)
B. (a + b)/2≥√ab
C. √(a² + b²)/2≥(a + b)/2
D. a² + b²≥2ab

答案： A