《2025年名校课堂九年级数学下册沪科版安徽专版》

10.（教材 P26 习题 T15 变式）小明不慎把家里的圆形玻璃打碎了，其中四块碎片如图所示，为配到与原来大小一样的圆形玻璃，小明带到商店去的一块玻璃碎片应该是 （ ）

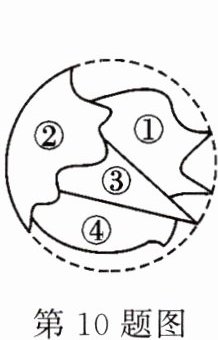
A. 第①块
B. 第②块
C. 第③块
D. 第④块

答案： B

11. 如图，在△ABC 中，AB = AC，AD 是∠BAC 的平分线，EF 是 AC 的垂直平分线，交 AD 于点 O. 若 OA = 3，则△ABC 外接圆的面积为 （ ）

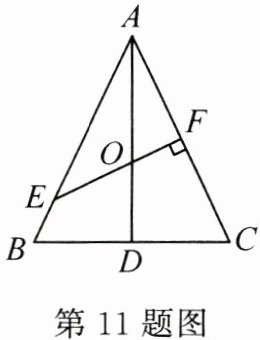
A. 3π
B. 4π
C. 6π
D. 9π

答案： D

12. 如图，⊙O 是等边三角形 ABC 的外接圆. 若 AB = 3，则⊙O 的半径是 （ ）

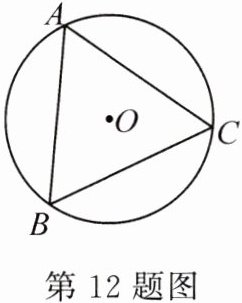
A. $\frac{3}{2}$
B. $\frac{\sqrt{3}}{2}$
C. $\sqrt{3}$
D. $\frac{5}{2}$

答案： C

13. 平面直角坐标系内的三个点 A(1，0)，B(0，－3)，C(2，－3) ______ 确定一个圆.（填“能”或“不能”）

答案： 能

14.（本课时 T12 变式）如图，在△ABC 中，∠B = 30°，∠C = 45°，AB = 4 cm. 能够将△ABC 完全覆盖的最小圆形纸片的面积是 ______________ cm².

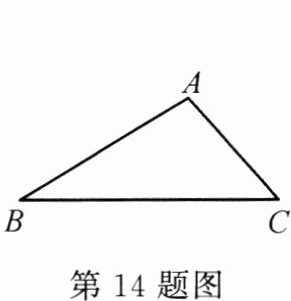
答案： $(4 + 2\sqrt{3})\pi$

15. 阅读下列文字，回答问题.
题目：在 Rt△ABC 中，∠C = 90°，若∠A≠45°，则 AC≠BC.
证明：假设 AC = BC，因为∠A≠45°，∠C = 90°，
所以∠A≠∠B.
所以 AC≠BC. 这与假设矛盾，所以 AC≠BC.
上面的证明有没有错误？若没有错误，指出其证明的方法；若有错误，请予以纠正.

答案： 解：有错误. 改正：假设AC = BC，则∠A = ∠B. 又因为∠C = 90°，所以∠B = ∠A = 45°. 这与∠A≠45°矛盾，所以AC = BC不成立. 所以AC≠BC.

16. 如图，残破的圆形轮片上，弦 AB 的垂直平分线交$\overset{\frown}{AB}$于点 C，交弦 AB 于点 D.
（1）用尺规作图的方法作此残片所在圆的圆心（不写作法，保留作图痕迹）；
（2）若 AB = 24，CD = 8，求此残片所在圆的半径.

答案： 解：（1）图略. （2）连接OB，根据垂径定理，得$BD=\frac{1}{2}AB = 12$，设半径为r，则OD = r - 8，OB = r，根据勾股定理，得$(r - 8)^2 + 12^2 = r^2$，解得r = 13. 答：此残片所在圆的半径为13.