第59页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
三、解答题(共46分)
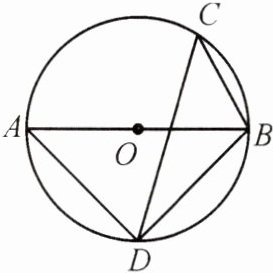
13.(10分)如图,AB是⊙O的直径,C,D两点在⊙O上,若∠BCD = 45°.
(1)求∠ABD的度数;
(2)若∠CDB = 30°,BC = 3,求⊙O的半径.
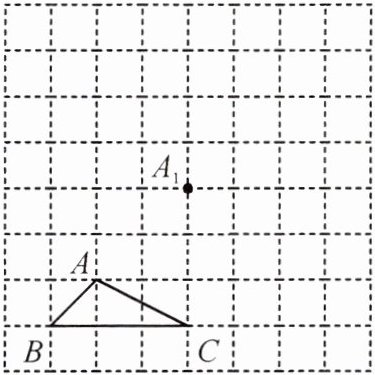
14.(11分)如图所示,在正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A₁,在网格中画出平移后得到的△A₁B₁C₁;
(2)把△A₁B₁C₁绕点A₁按逆时针方向旋转90°,在网格中画出旋转后的△A₁B₂C₂;
(3)如果网格中小正方形的边长为1,求点B经过(1)(2)变换的路径总长.
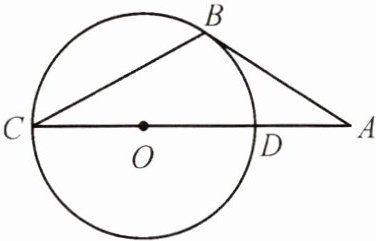
15.(12分)如图,已知CD是⊙O的直径,点A为CD延长线上一点,BC = AB,∠A = 30°.
(1)求证:AB是⊙O的切线;
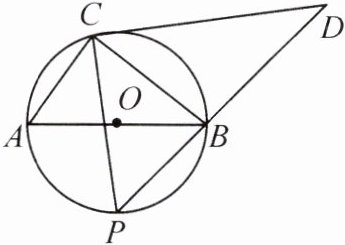
16.(13分)如图,AB是⊙O的直径,在AB的异侧分别有定点C和动点P,点P在半圆弧AB上运动(不与点A,B重合),过点C作CP的垂线CD,交PB的延长线于点D. 已知AB = 5,BC∶CA = 4∶3.
(1)求证:AC·CD = PC·BC;
(2)当点P运动到$\overset{\frown}{AB}$的中点时,求CD的长;
(3)当点P运动到什么位置时,△PCD的面积最大?请直接写出这个最大面积.
13.(10分)如图,AB是⊙O的直径,C,D两点在⊙O上,若∠BCD = 45°.
(1)求∠ABD的度数;
(2)若∠CDB = 30°,BC = 3,求⊙O的半径.

14.(11分)如图所示,在正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A₁,在网格中画出平移后得到的△A₁B₁C₁;
(2)把△A₁B₁C₁绕点A₁按逆时针方向旋转90°,在网格中画出旋转后的△A₁B₂C₂;
(3)如果网格中小正方形的边长为1,求点B经过(1)(2)变换的路径总长.

15.(12分)如图,已知CD是⊙O的直径,点A为CD延长线上一点,BC = AB,∠A = 30°.
(1)求证:AB是⊙O的切线;

16.(13分)如图,AB是⊙O的直径,在AB的异侧分别有定点C和动点P,点P在半圆弧AB上运动(不与点A,B重合),过点C作CP的垂线CD,交PB的延长线于点D. 已知AB = 5,BC∶CA = 4∶3.
(1)求证:AC·CD = PC·BC;
(2)当点P运动到$\overset{\frown}{AB}$的中点时,求CD的长;
(3)当点P运动到什么位置时,△PCD的面积最大?请直接写出这个最大面积.

答案:
解:
(1) 因为$\angle BCD = 45^{\circ}$,所以$\angle BAD=\angle BCD = 45^{\circ}$。因为$AB$是$\odot O$的直径,所以$\angle ADB = 90^{\circ}$,所以$\angle ABD = 45^{\circ}$。
(2) 连接$AC$,因为$AB$是$\odot O$的直径,所以$\angle ACB = 90^{\circ}$。因为$\angle CAB=\angle CDB = 30^{\circ}$,$BC = 3$,所以$AB = 6$,所以$\odot O$的半径为3。@@解:
(1) 图略。
(2) 图略。
(3) 点$B$到$B_1$的路径长是$\sqrt{2^{2}+2^{2}}=2\sqrt{2}$,点$B_1$到$B_2$的路径长是$\frac{90\pi\times\sqrt{2}}{180}=\frac{\sqrt{2}}{2}\pi$。则路径总长是$2\sqrt{2}+\frac{\sqrt{2}}{2}\pi$。@@解:
(1) 证明:连接$OB$,因为$BC = AB$,$\angle A = 30^{\circ}$,所以$\angle C=\angle A = 30^{\circ}$。又因为$OC = OB$,所以$\angle CBO=\angle C = 30^{\circ}$,所以$\angle AOB=\angle CBO+\angle C = 60^{\circ}$。在$\triangle ABO$中,$\angle A = 30^{\circ}$,$\angle AOB = 60^{\circ}$,所以$\angle ABO = 90^{\circ}$,即$AB\perp OB$。又因为$OB$是$\odot O$的半径,所以$AB$为$\odot O$的切线。
(2) 因为$OB = 2$,$\angle BOD = 60^{\circ}$,所以$l_{\overset{\frown}{BD}}=\frac{60\pi\times2}{180}=\frac{2}{3}\pi$。@@解:
(1) 证明:因为$AB$为直径,所以$\angle ACB = 90^{\circ}$。因为$PC\perp CD$,所以$\angle PCD = 90^{\circ}$,所以$\angle PCD=\angle ACB$。因为$\angle A=\angle P$,所以$\triangle ABC\sim\triangle PDC$,所以$\frac{AC}{PC}=\frac{BC}{CD}$,所以$AC\cdot CD = PC\cdot BC$。
(2) 因为$AB = 5$,$BC:CA = 4:3$,$\angle ACB = 90^{\circ}$,所以$BC = 4$,$AC = 3$。当点$P$运动到$\overset{\frown}{AB}$的中点时,过点$B$作$BE\perp PC$于点$E$,因为点$P$是$\overset{\frown}{AB}$的中点,所以$\angle PCB = 45^{\circ}$,且$BC = 4$,所以$CE = BE=\frac{\sqrt{2}}{2}BC = 2\sqrt{2}$。因为$\angle CAB=\angle CPB$,所以$\tan A=\tan P=\frac{BC}{AC}=\frac{BE}{PE}=\frac{4}{3}$,所以$PE=\frac{3\sqrt{2}}{2}$,所以$PC = PE + CE=\frac{3\sqrt{2}}{2}+2\sqrt{2}=\frac{7\sqrt{2}}{2}$。因为$AC\cdot CD = PC\cdot BC$,所以$3CD=\frac{7\sqrt{2}}{2}\times4$,所以$CD=\frac{14\sqrt{2}}{3}$。
(3) $\frac{50}{3}$。
(1) 因为$\angle BCD = 45^{\circ}$,所以$\angle BAD=\angle BCD = 45^{\circ}$。因为$AB$是$\odot O$的直径,所以$\angle ADB = 90^{\circ}$,所以$\angle ABD = 45^{\circ}$。
(2) 连接$AC$,因为$AB$是$\odot O$的直径,所以$\angle ACB = 90^{\circ}$。因为$\angle CAB=\angle CDB = 30^{\circ}$,$BC = 3$,所以$AB = 6$,所以$\odot O$的半径为3。@@解:
(1) 图略。
(2) 图略。
(3) 点$B$到$B_1$的路径长是$\sqrt{2^{2}+2^{2}}=2\sqrt{2}$,点$B_1$到$B_2$的路径长是$\frac{90\pi\times\sqrt{2}}{180}=\frac{\sqrt{2}}{2}\pi$。则路径总长是$2\sqrt{2}+\frac{\sqrt{2}}{2}\pi$。@@解:
(1) 证明:连接$OB$,因为$BC = AB$,$\angle A = 30^{\circ}$,所以$\angle C=\angle A = 30^{\circ}$。又因为$OC = OB$,所以$\angle CBO=\angle C = 30^{\circ}$,所以$\angle AOB=\angle CBO+\angle C = 60^{\circ}$。在$\triangle ABO$中,$\angle A = 30^{\circ}$,$\angle AOB = 60^{\circ}$,所以$\angle ABO = 90^{\circ}$,即$AB\perp OB$。又因为$OB$是$\odot O$的半径,所以$AB$为$\odot O$的切线。
(2) 因为$OB = 2$,$\angle BOD = 60^{\circ}$,所以$l_{\overset{\frown}{BD}}=\frac{60\pi\times2}{180}=\frac{2}{3}\pi$。@@解:
(1) 证明:因为$AB$为直径,所以$\angle ACB = 90^{\circ}$。因为$PC\perp CD$,所以$\angle PCD = 90^{\circ}$,所以$\angle PCD=\angle ACB$。因为$\angle A=\angle P$,所以$\triangle ABC\sim\triangle PDC$,所以$\frac{AC}{PC}=\frac{BC}{CD}$,所以$AC\cdot CD = PC\cdot BC$。
(2) 因为$AB = 5$,$BC:CA = 4:3$,$\angle ACB = 90^{\circ}$,所以$BC = 4$,$AC = 3$。当点$P$运动到$\overset{\frown}{AB}$的中点时,过点$B$作$BE\perp PC$于点$E$,因为点$P$是$\overset{\frown}{AB}$的中点,所以$\angle PCB = 45^{\circ}$,且$BC = 4$,所以$CE = BE=\frac{\sqrt{2}}{2}BC = 2\sqrt{2}$。因为$\angle CAB=\angle CPB$,所以$\tan A=\tan P=\frac{BC}{AC}=\frac{BE}{PE}=\frac{4}{3}$,所以$PE=\frac{3\sqrt{2}}{2}$,所以$PC = PE + CE=\frac{3\sqrt{2}}{2}+2\sqrt{2}=\frac{7\sqrt{2}}{2}$。因为$AC\cdot CD = PC\cdot BC$,所以$3CD=\frac{7\sqrt{2}}{2}\times4$,所以$CD=\frac{14\sqrt{2}}{3}$。
(3) $\frac{50}{3}$。
15.(12分)如图,已知CD是⊙O的直径,点A为CD延长线上一点,BC = AB,∠A = 30°.
(1)求证:AB是⊙O的切线;

(1)求证:AB是⊙O的切线;
(2)若⊙O的半径为2,求BD的长.

答案:
解:
(1) 证明:连接$OB$,因为$BC = AB$,$\angle A = 30^{\circ}$,所以$\angle C=\angle A = 30^{\circ}$。又因为$OC = OB$,所以$\angle CBO=\angle C = 30^{\circ}$,所以$\angle AOB=\angle CBO+\angle C = 60^{\circ}$。在$\triangle ABO$中,$\angle A = 30^{\circ}$,$\angle AOB = 60^{\circ}$,所以$\angle ABO = 90^{\circ}$,即$AB\perp OB$。又因为$OB$是$\odot O$的半径,所以$AB$为$\odot O$的切线。
(2) 因为$OB = 2$,$\angle BOD = 60^{\circ}$,所以$l_{\overset{\frown}{BD}}=\frac{60\pi\times2}{180}=\frac{2}{3}\pi$。
(1) 证明:连接$OB$,因为$BC = AB$,$\angle A = 30^{\circ}$,所以$\angle C=\angle A = 30^{\circ}$。又因为$OC = OB$,所以$\angle CBO=\angle C = 30^{\circ}$,所以$\angle AOB=\angle CBO+\angle C = 60^{\circ}$。在$\triangle ABO$中,$\angle A = 30^{\circ}$,$\angle AOB = 60^{\circ}$,所以$\angle ABO = 90^{\circ}$,即$AB\perp OB$。又因为$OB$是$\odot O$的半径,所以$AB$为$\odot O$的切线。
(2) 因为$OB = 2$,$\angle BOD = 60^{\circ}$,所以$l_{\overset{\frown}{BD}}=\frac{60\pi\times2}{180}=\frac{2}{3}\pi$。
查看更多完整答案,请扫码查看


