《2025年名校课堂九年级数学下册沪科版安徽专版》

1. 下列说法：①圆是轴对称图形；②圆有无数条对称轴；③圆的任意一条直径都是圆的对称轴；④圆所在平面内任意一条经过圆心的直线都是圆的对称轴. 其中正确的有 （ ）
A. 1 个
B. 2 个
C. 3 个
D. 4 个

答案： C

2. 如图，AB 是⊙O 的直径，弦 CD⊥AB，垂足为 M，下列结论不成立的是 （ ）

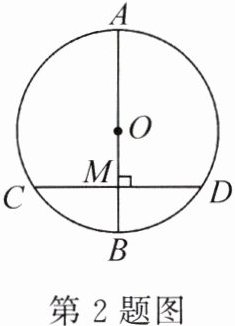
A. CM = DM
B. $\overset{\frown}{CB}=\overset{\frown}{BD}$
C. $\overset{\frown}{AC}=\overset{\frown}{AD}$
D. OM = MD

答案： D

3.（2024·长沙）如图，在⊙O 中，弦 AB 的长为 8，圆心 O 到 AB 的距离 OE = 4，则⊙O 的半径长为 （ ）

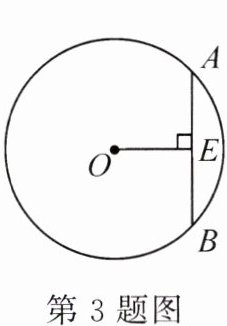
A. 4
B. 4 $\sqrt{2}$
C. 5
D. 5 $\sqrt{2}$

答案： B

4.（2024·新疆）如图，AB 是⊙O 的直径，CD 是⊙O 的弦，AB⊥CD，垂足为 E. 若 CD = 8，OD = 5，则 BE 的长为 （ ）

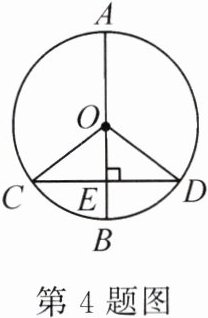
A. 1
B. 2
C. 3
D. 4

答案： B

5. 如图，在⊙O 中，C 是弦 AB 的中点，且 AC = 2，连接 OC，线段 OC 的长为 2，则∠AOC 的度数为______.

答案： 45°

6. 如图，将半径为 2 cm 的圆形纸片折叠后，圆弧恰好经过圆心 O，则折痕 AB 的长为__________.

答案： 2√3 cm

7. 如图所示，在⊙O 中，AB，CD 为两条弦，且 AB//CD，直径 MN 经过 AB 的中点 E，交 CD 于点 F，试问：点 F 是 CD 的中点吗？

答案： 解：点F是CD的中点. 理由：
∵直径MN平分不是直径的弦AB，
∴MN⊥AB.
∵AB//CD，
∴MN⊥CD.
∴CF = FD.
∴点F是CD的中点.

8. 一条排水管的截面如图所示，已知排水管的直径为 10，水面宽 AB = 8，则截面圆心 O 到水面的距离 OC 的长为 （ ）

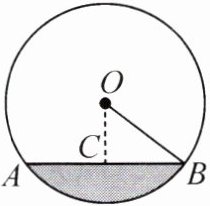
A. 4
B. 3
C. 2
D. 1

答案： B

9.【情境素材题】（教材 P16 例 3 变式）被誉为“中国画里乡村”的黄山宏村，村头有一座美丽的圆弧形石拱桥（如图），已知桥拱的顶部 C 距水面的距离 CD 为 2.7 m，桥拱所在的圆的半径 OC 为 1.5 m，则水面 AB 的宽度是 （ ）

A. 1.8 m
B. 1.6 m
C. 1.2 m
D. 0.9 m

答案： A