《2025年名校课堂九年级数学下册沪科版安徽专版》

11. 如图，直线$y = -\frac{4}{3}x + 4$与x轴、y轴分别交于A，B两点，把△AOB绕点A顺时针旋转90°后得到△AO′B′，则点B′的坐标是__________.

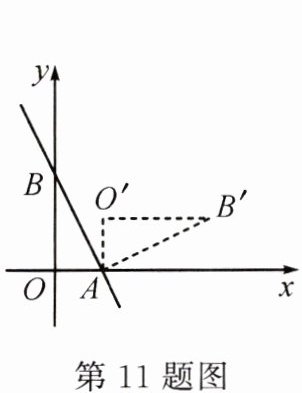
答案： (7, 3)

12. 如图，在矩形ABCD中，AB = 2，BC = 1，将矩形ABCD绕点A顺时针旋转90°得矩形AEFG，连接CG，EG，则∠CGE = _______.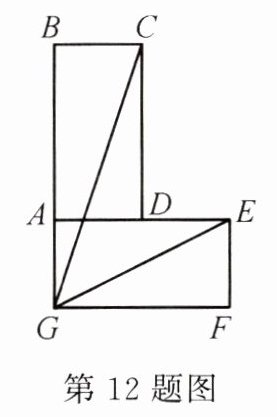

答案： $45^{\circ}$

13.（10分）如图，方格纸中的每个小方格都是边长为1的正方形，建立平面直角坐标系后，△ABC的顶点都在格点上.
（1）画出△ABC关于原点O对称的△A₁B₁C₁；
（2）画出△ABC绕点B顺时针旋转90°后的△A₂BC₂，点C₂的坐标为___________.

答案： (2, -1)

14.（14分）如图，AC⊥BC，垂足为C，AC = 6，$BC = 4\sqrt{3}$，将线段AC绕点C按顺时针方向旋转60°，得到线段CD，连接AD，DB.
（1）求线段BD的长；
（2）求四边形ACBD的面积.

答案： 解：
(1)由旋转的性质，得 $AC = CD = 6$，$\angle ACD = 60^{\circ}$，$\therefore$ $\triangle ACD$是等边三角形. 过点 $D$作 $DE\perp BC$于点 $E$. $\because AC\perp BC$，$\therefore\angle DCE=\angle ACB - \angle ACD = 90^{\circ} - 60^{\circ} = 30^{\circ}$. $\therefore$在 $Rt\triangle CDE$中，$DE = \frac{1}{2}CD = 3$，$CE = \sqrt{3}DE = 3\sqrt{3}$. $\therefore BE = BC - CE = \sqrt{3}$. $\therefore BD = \sqrt{BE^{2} + DE^{2}} = 2\sqrt{3}$.
(2) $S_{四边形ACBD}=S_{\triangle ACD}+S_{\triangle BCD}=\frac{1}{2}\times\frac{\sqrt{3}}{2}\times6\times6+\frac{1}{2}\times4\sqrt{3}\times3 = 15\sqrt{3}$.

15.（16分）如图1所示放置的一副三角板，将含45°角的三角板以斜边中点O为旋转中心，逆时针旋转30°，如图2，连接OB，OD，AD.
（1）求证：△AOB≌△AOD；
（2）试判定四边形ABOD是什么四边形？并说明理由.

答案： 解：
(1)证明：根据题意，得 $\angle BAC = 60^{\circ}$，$\angle ABC = \angle EDF = 90^{\circ}$，$EF = AC$，$OD\perp EF$，$\because O$为 $AC$，$EF$的中点，$\therefore OB = \frac{1}{2}AC$，$OD = \frac{1}{2}EF$. 又 $\because AC = EF$，$\therefore OB = OD = OA$. $\because$ $\angle BAO = 60^{\circ}$，$\therefore\triangle AOB$是等边三角形. $\therefore\angle AOB = 60^{\circ}$，$AB = OB = OA$. $\because\triangle DEF$绕斜边中点 $O$逆时针旋转 $30^{\circ}$得到图2，$\therefore\angle AOE = 30^{\circ}$. $\therefore\angle AOD = 90^{\circ} - 30^{\circ} = 60^{\circ}$. $\therefore\triangle AOD$为等边三角形. $\therefore\triangle AOB\cong\triangle AOD$.
(2)四边形 $ABOD$是菱形. 理由：$\because\triangle AOB\cong\triangle AOD$，$\therefore AB = AD$. $\therefore AB = AD = OB = OD$. $\therefore$四边形 $ABOD$是菱形.