《2025年名校课堂九年级数学下册沪科版安徽专版》

8. 用频率估计概率，可以发现，某种幼树在一定条件下移植成活的概率为 0.9，下列说法正确的是 （ ）
A. 种植 10 棵幼树，结果一定是“有 9 棵幼树成活”
B. 种植 100 棵幼树，结果一定是“90 棵幼树成活”和“10 棵幼树不成活”
C. 种植 10n 棵幼树，恰好有“n 棵幼树不成活”
D. 种植 n 棵幼树，当 n 越来越大时，种植成活幼树的频率会越来越稳定于 0.9

答案： D

9. 一个不透明的袋子里装有黑、白两种颜色的球共 50 只，这些球除颜色外都相同. 小明从袋子中随机摸一个球，记下颜色后放回，不断重复，并绘制了如图所示的统计图，根据统计图提供的信息解决下列问题：

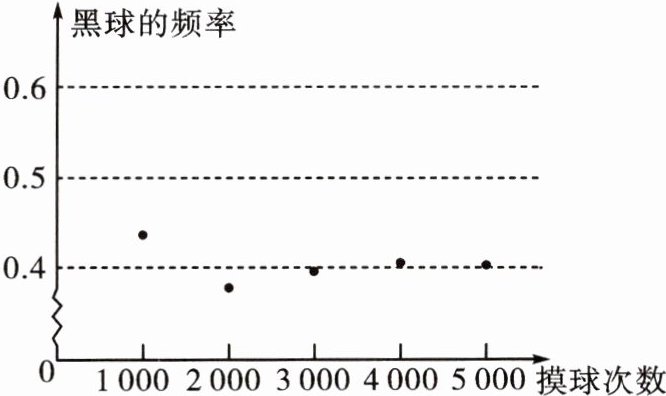
（1）摸到黑球的频率接近______（精确到 0.1），估计摸一次球能摸到黑球的概率是______；袋中黑球的个数约为______；
（2）若小明又将一些相同的黑球放进了这个不透明的袋子里，然后再次进行摸球试验，当重复大量试验后，发现黑球的频率稳定在 0.6 左右，则小明后来放进了______个黑球.

答案： 0.4@@0.4@@20@@25

10. 给出下列四个命题：
①设有一批产品，其次品率为 0.05，则从中任取 200 件，必有 10 件是次品；
②做 100 次抛硬币的试验，结果 51 次出现正面朝上，因此，出现正面朝上的概率是$\frac{51}{100}$；
③随机事件发生的频率就是这个随机事件发生的概率；
④抛掷骰子 100 次，得到的点数是 1 的结果有 18 次，则出现 1 点的频率是$\frac{9}{50}$.
其中正确命题有______.

答案： ④

11. 为响应绿色出行，某市在推出“共享单车”后，又推出“新能源租赁汽车”. 每次租车收费的标准由两部分组成：①里程计费：1 元/千米；②时间计费：0.1 元/分. 已知陈先生的家离上班公司 20 千米，每天上下班租用该款汽车各一次. 一次路上开车所用的时间记为 t（分），现统计了 50 次路上开车所用时间，在各时间段内频数分布情况如表所示：
|时间 t/分|25≤t＜35|35≤t＜45|45≤t＜55|55≤t＜65|
|----|----|----|----|----|
|次数|10|28|8|4|
将各时间段发生的频率视为概率，一次路上开车所用的时间视为用车时间，范围为 25≤t＜65.
（1）估计陈先生一次租用新能源租赁汽车所用的时间不低于 35 分钟的概率为______；
（2）若公司每月发放 1 000 元的交通补助费用，则这笔钱______（填“够”或“不够”）让陈先生一个月上下班租用新能源租赁汽车（每月按 22 天计算）.

答案： 0.8@@不够