第74页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
1. 将正面分别标有数字-1,2,3,4 的四张卡片(除数字外其余都相同)洗匀后,背面朝上放置在桌面上.
(1) 小明从这四张卡片中随机抽取一张,抽到一张恰好是正数的概率是 ________ ;
(2) 随机抽出一张,记其数字为 b,不放回,再随机抽出一张,记其数字为 c,则使关于 x 的方程$x^{2}+bx + c = 0$有实数根的概率是多少?
(1) 小明从这四张卡片中随机抽取一张,抽到一张恰好是正数的概率是 ________ ;
(2) 随机抽出一张,记其数字为 b,不放回,再随机抽出一张,记其数字为 c,则使关于 x 的方程$x^{2}+bx + c = 0$有实数根的概率是多少?
答案:
解:
(1)$\frac{3}{4}$
(2)画树状图如下: 开始 |--b | |-- -1 | | |-- 2 | | |-- 3 | | |-- 4 | |-- 2 | | |-- -1 | | |-- 3 | | |-- 4 | |-- 3 | | |-- -1 | | |-- 2 | | |-- 4 | |-- 4 | |-- -1 | |-- 2 | |-- 3 $b^{2}-4c\geq0$ √ √ √ √ √ √
∵共有12种等可能结果,其中满足方程$x^{2}+bx + c = 0$有实数根的结果有6种,
∴$P$(方程$x^{2}+bx + c = 0$有实数根)=$\frac{6}{12}=\frac{1}{2}$。
(1)$\frac{3}{4}$
(2)画树状图如下: 开始 |--b | |-- -1 | | |-- 2 | | |-- 3 | | |-- 4 | |-- 2 | | |-- -1 | | |-- 3 | | |-- 4 | |-- 3 | | |-- -1 | | |-- 2 | | |-- 4 | |-- 4 | |-- -1 | |-- 2 | |-- 3 $b^{2}-4c\geq0$ √ √ √ √ √ √
∵共有12种等可能结果,其中满足方程$x^{2}+bx + c = 0$有实数根的结果有6种,
∴$P$(方程$x^{2}+bx + c = 0$有实数根)=$\frac{6}{12}=\frac{1}{2}$。
2. 如图所示的四枚邮票图片形状完全相同,分别是我国古代科学家祖冲之、李时珍、张衡、僧一行,把四张图片混合在一起.

(1) 若随机摸取一张图片,则摸到“祖冲之”图片的概率是 ________ ;
(2) 若随机摸取一张图片然后放回,再随机摸取一张图片,利用列表或画树状图法求两次至少有一次摸到“祖冲之”图片的概率;
(3) 小东、小西、小南、小北四位同学依次摸取图片,若小东摸到“祖冲之”图片,则剩下三人中 _____.
A. 小西摸到“李时珍”图片的概率大
B. 小南摸到“李时珍”图片的概率大
C. 小北摸到“李时珍”图片的概率大
D. 三人摸到“李时珍”图片的概率一样大

(1) 若随机摸取一张图片,则摸到“祖冲之”图片的概率是 ________ ;
(2) 若随机摸取一张图片然后放回,再随机摸取一张图片,利用列表或画树状图法求两次至少有一次摸到“祖冲之”图片的概率;
(3) 小东、小西、小南、小北四位同学依次摸取图片,若小东摸到“祖冲之”图片,则剩下三人中 _____.
A. 小西摸到“李时珍”图片的概率大
B. 小南摸到“李时珍”图片的概率大
C. 小北摸到“李时珍”图片的概率大
D. 三人摸到“李时珍”图片的概率一样大
答案:
解:
(1)$\frac{1}{4}$
(2)用A,B,C,D分别表示“祖冲之、李时珍、张衡、僧一行”图片,列表如下: |第2次|第1次| |----|----| | |A|B|C|D| |A|(A,A)|(B,A)|(C,A)|(D,A)| |B|(A,B)|(B,B)|(C,B)|(D,B)| |C|(A,C)|(B,C)|(C,C)|(D,C)| |D|(A,D)|(B,D)|(C,D)|(D,D)| 所有等可能的结果共有16种,其中至少有一次摸到“祖冲之”图片的结果有7种,
∴$P$(至少有一次摸到“祖冲之”图片)=$\frac{7}{16}$。
(3)D
(1)$\frac{1}{4}$
(2)用A,B,C,D分别表示“祖冲之、李时珍、张衡、僧一行”图片,列表如下: |第2次|第1次| |----|----| | |A|B|C|D| |A|(A,A)|(B,A)|(C,A)|(D,A)| |B|(A,B)|(B,B)|(C,B)|(D,B)| |C|(A,C)|(B,C)|(C,C)|(D,C)| |D|(A,D)|(B,D)|(C,D)|(D,D)| 所有等可能的结果共有16种,其中至少有一次摸到“祖冲之”图片的结果有7种,
∴$P$(至少有一次摸到“祖冲之”图片)=$\frac{7}{16}$。
(3)D
3.(2020·安徽)某单位食堂为全体 960 名职工提供了 A,B,C,D 四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取 240 名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查. 根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
调查结果的条形统计图 调查结果的扇形统计图
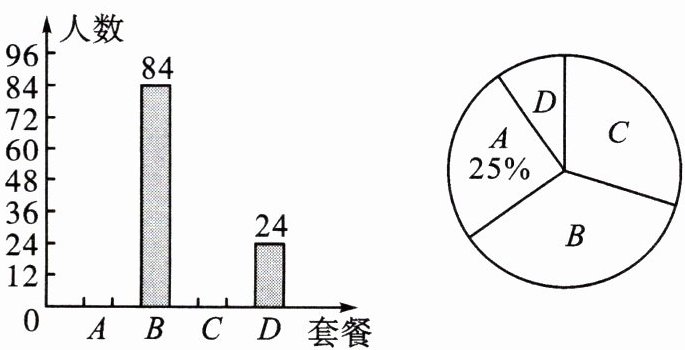
(1) 在抽取的 240 人中最喜欢 A 套餐的人数为 _____,扇形统计图中“C”对应扇形的圆心角的大小为 ______°;
(2) 依据本次调查的结果,估计全体 960 名职工中最喜欢 B 套餐的人数;
(3) 现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.
调查结果的条形统计图 调查结果的扇形统计图

(1) 在抽取的 240 人中最喜欢 A 套餐的人数为 _____,扇形统计图中“C”对应扇形的圆心角的大小为 ______°;
(2) 依据本次调查的结果,估计全体 960 名职工中最喜欢 B 套餐的人数;
(3) 现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.
答案:
解:
(1)60 108
(2)估计全体960名职工中最喜欢B套餐的人数为$960\times\frac{84}{240}=336$(人)。
(3)画树状图为: 甲 |--乙 | |--丙 | |--丁 |--丙 | |--甲 | |--丁 |--丁 | |--甲 | |--乙 乙 |--甲 | |--丙 | |--丁 |--丙 | |--甲 | |--丁 |--丁 | |--甲 | |--乙 丙 |--甲 | |--乙 | |--丁 |--乙 | |--甲 | |--丁 |--丁 | |--甲 | |--乙 丁 |--甲 | |--乙 | |--丙 |--乙 | |--甲 | |--丙 |--丙 | |--甲 | |--乙 共有12种等可能的结果数,其中甲被选到的结果数为6.
∴甲被选到的概率为$\frac{6}{12}=\frac{1}{2}$。
(1)60 108
(2)估计全体960名职工中最喜欢B套餐的人数为$960\times\frac{84}{240}=336$(人)。
(3)画树状图为: 甲 |--乙 | |--丙 | |--丁 |--丙 | |--甲 | |--丁 |--丁 | |--甲 | |--乙 乙 |--甲 | |--丙 | |--丁 |--丙 | |--甲 | |--丁 |--丁 | |--甲 | |--乙 丙 |--甲 | |--乙 | |--丁 |--乙 | |--甲 | |--丁 |--丁 | |--甲 | |--乙 丁 |--甲 | |--乙 | |--丙 |--乙 | |--甲 | |--丙 |--丙 | |--甲 | |--乙 共有12种等可能的结果数,其中甲被选到的结果数为6.
∴甲被选到的概率为$\frac{6}{12}=\frac{1}{2}$。
查看更多完整答案,请扫码查看


