《2025年名校课堂九年级数学下册沪科版安徽专版》

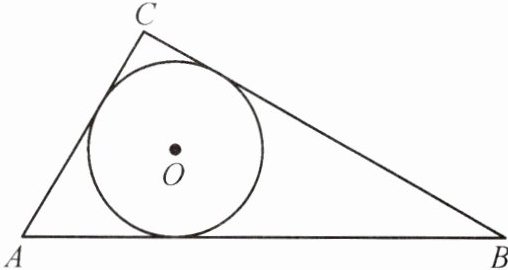
1. 如图，$\odot O$是$\triangle ABC$的内切圆，则点$O$是$\triangle ABC$的 （ ）

A. 三条边的垂直平分线的交点
B. 三条角平分线的交点
C. 三条中线的交点
D. 三条高的交点

答案： B

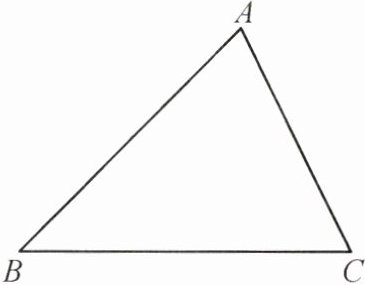
2. 制作铁皮桶，需在一块三角形材料上截取一个面积最大的圆，请画出该圆.（要求尺规作图，保留作图痕迹，不要求写作法）

答案： 解：图略。

3. 若三角形的内心和外心重合，则这个三角形是 （ ）
A. 直角三角形
B. 等腰直角三角形
C. 等腰三角形
D. 等边三角形

答案： D

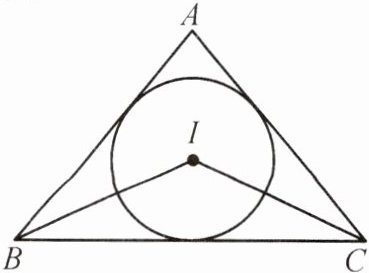
4. 如图，点$I$是$\triangle ABC$的内心，$\angle BIC = 130^{\circ}$，则$\angle BAC$的度数为 （ ）

A. $65^{\circ}$
B. $50^{\circ}$
C. $80^{\circ}$
D. $100^{\circ}$

答案： C

5. 如果$\triangle ABC$的三边长分别为$a$，$b$，$c$，它的内切圆半径为$r$，那么$\triangle ABC$的面积为 （ ）
A. $(a + b + c)\cdot r$
B. $\frac{1}{2}(a + b + c)\cdot r$
C. $\frac{1}{3}(a + b + c)\cdot r$
D. $\frac{1}{4}(a + b + c)\cdot r$

答案： B

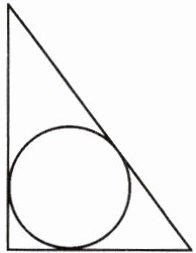
6. 《九章算术》中有一题“今有勾五步，股十二步，问勾中容圆径几何？”其意思是：今有直角三角形，勾（短直角边）长为$5$步，股（长直角边）长为$12$步，问该直角三角形能容纳的圆形（内切圆）直径是多少步？答：______步.

答案： 4

7. （教材P44习题T2变式）如图，在$\triangle ABC$内，内切圆$\odot O$分别与$BC$，$AC$，$AB$相切于点$D$，$E$，$F$. 若$\angle FDE = 65^{\circ}$，求$\angle A$的度数.

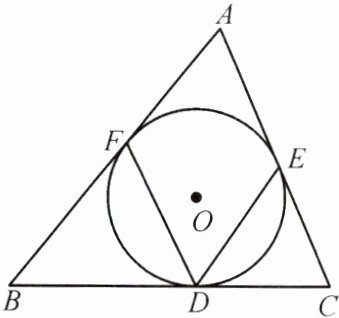
答案： 解：连接 OE，OF。因为 AB，AC 分别是⊙O 的切线，所以∠AEO = ∠AFO = 90°。所以∠A + ∠EOF = 180°。因为∠EOF = 2∠EDF = 130°，所以∠A = 180° - ∠EOF = 50°。

8. （教材P44习题T3变式）如图，$\odot O$是$\triangle ABC$的内切圆，切点分别为点$D$，$E$，$F$，$AB = AC = 13$，$BC = 10$. 求$\odot O$的半径.

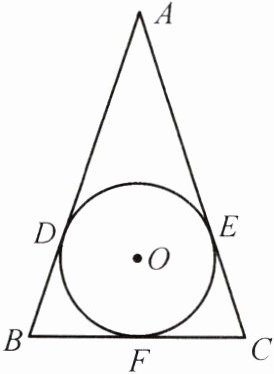
答案： 解：连接 AF。因为⊙O 是△ABC 的内切圆，所以 AD = AE，BD = BF，CF = CE。因为 AB = AC，所以 BD = CE。所以 BF = CF。所以 BF = $\frac{1}{2}$BC = $\frac{1}{2}$×10 = 5，AF⊥BC。所以 AF = $\sqrt{AB^{2}-BF^{2}}$ = 12。所以$S_{\triangle ABC}$ = $\frac{1}{2}$BC·AF = $\frac{1}{2}$×10×12 = 60。设⊙O 的半径是 r，则$\frac{1}{2}$×(13 + 13 + 10)·r = 60，解得 r = $\frac{10}{3}$。所以⊙O 的半径为$\frac{10}{3}$。