《2025年名校课堂九年级数学下册沪科版安徽专版》

1. 船在航行过程中，船长常常通过测定角度来确定是否会遇到暗礁. 如图，A，B表示灯塔，暗礁分布在经过A，B两点的一个圆形区域内，优弧AB上任一点C都是有触礁危险的临界点，∠ACB就是“危险角”. 当船P位于安全区域时，它与两个灯塔的夹角∠α与“危险角”∠ACB的大小关系为 （ ）

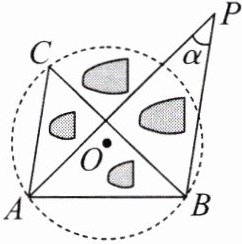
A. ∠α＞∠ACB
B. ∠α＜∠ACB
C. ∠α＝∠ACB
D. 不确定

答案： B

2. 草锅盖，又名盖顶，是一种以牛筋草、江边草和斑茅草为原材料进行编织缠绕的云南特有的传统草编工艺品. 某兴趣小组根据草锅盖的特征制作了一个圆锥模型，并用测量工具测量其尺寸，如图所示，由图中的数据可知圆锥模型的侧面积为______cm².

答案： $20\pi$

3. 我国魏晋时期数学家刘徽在《九章算术注》中提出了著名的“割圆术”. 所谓“割圆术”，是用圆内接正多边形的面积去无限逼近圆的面积，并以此求取圆周率π的方法. 刘徽指出“割之弥细，所失弥少. 割之又割，以至于不可割，则与圆周合体，而无所失矣”. 例如：⊙O的半径为1，运用“割圆术”，以圆内接正六边形面积估计⊙O的面积，S正六边形 = 6×$\frac{1}{2}$×1×$\frac{\sqrt{3}}{2}$ = $\frac{3\sqrt{3}}{2}$，所以⊙O的面积近似为$\frac{3\sqrt{3}}{2}$，由此可得π的估计值为$\frac{3\sqrt{3}}{2}$. 若用圆内接正十二边形估计⊙O的面积，可得π的估计值为______.

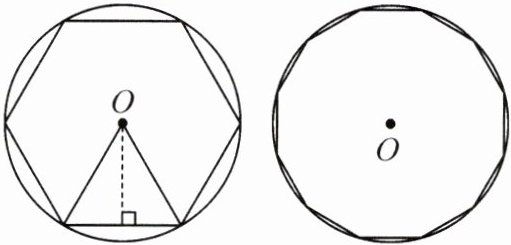
答案： 3

4.（2024·安徽模拟）如图1所示的是我国明末《崇祯历书》之《割圆勾股八线表》中所绘的割圆八线图. 如图2，根据割圆八线图，在扇形AOB中，∠AOB = 90°，AC和BE都是⊙O的切线，点A和点B是切点，BE交OC于点E，OC交⊙O于点D，AD = CD. 若OA = 3，则CE的长为__________.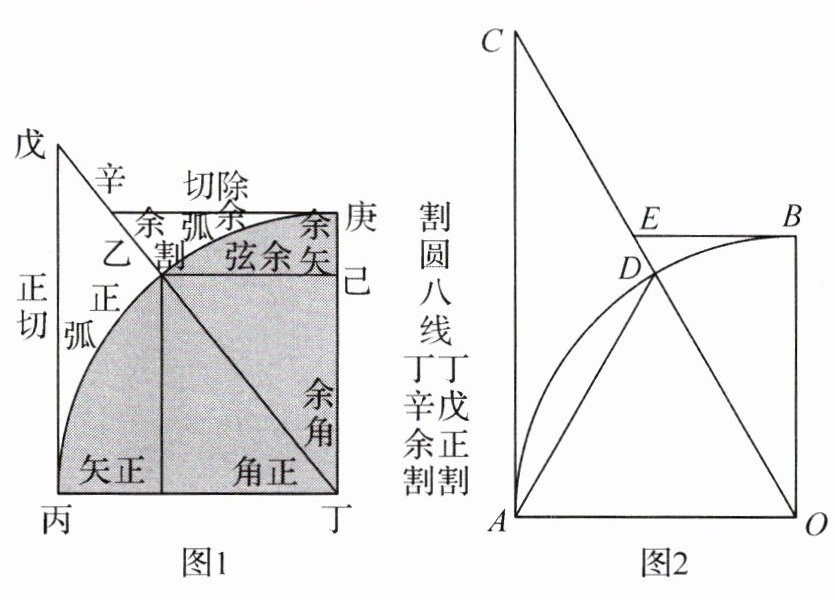

答案： $6 - 2\sqrt{3}$

5.（2024·合肥蜀山区模拟）苯（分子式为C₆H₆）的环状结构是由德国化学家凯库勒提出的. 随着研究的不断深入，发现阳苯分子中的6个碳原子组成了一个完美的正六边形（如图1），图2是其平面示意图，点O为正六边形ABCDEF的中心，则∠CBF - ∠COD的度数为 （ ）


A. 30°
B. 45°
C. 60°
D. 90°

答案： A