第11页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
10.(2024·安徽模拟)如图,在等边三角形ABC
中,CD为边AB上的高,M是直线CD上的
一个动点,连接MB,将线段BM绕点B逆
时针旋转60°得到线段BN,连接DN.若
AB = 5,则在点M的运动过程中,线段DN
的长的最小值是 ( )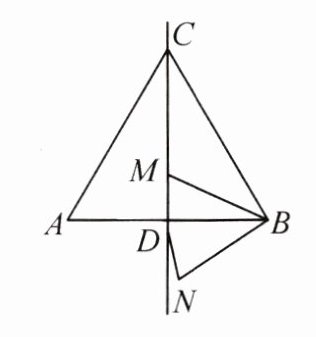
A. 2
B. $\frac{5}{4}$
C. $\frac{5}{2}$
D. $\frac{5\sqrt{3}}{2}$
中,CD为边AB上的高,M是直线CD上的
一个动点,连接MB,将线段BM绕点B逆
时针旋转60°得到线段BN,连接DN.若
AB = 5,则在点M的运动过程中,线段DN
的长的最小值是 ( )

A. 2
B. $\frac{5}{4}$
C. $\frac{5}{2}$
D. $\frac{5\sqrt{3}}{2}$
答案:
B
11. 如图,在矩形ABCD中,BC = 4,将矩形ABCD
绕点C顺时针旋转得到矩形A'B'C'D'.当点
B'恰好落在边AD上时,旋转角为α,连接
BB'.若∠AB'B = 75°,求旋转角α及AB
的长.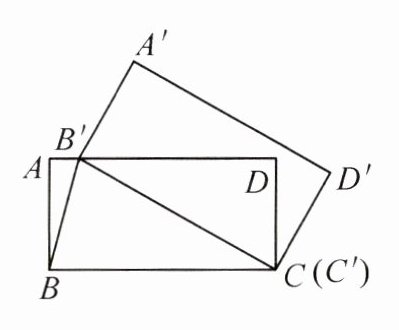
绕点C顺时针旋转得到矩形A'B'C'D'.当点
B'恰好落在边AD上时,旋转角为α,连接
BB'.若∠AB'B = 75°,求旋转角α及AB
的长.

答案:
解:四边形ABCD是矩形,
∴AD//BC.
∴∠CBB' = ∠AB'B = 75°. 由旋转的性质,得CB = CB',
∴∠CB'B = ∠CBB' = 75°.
∴∠BCB' = 180° - 75° - 75° = 30°,即旋转角α = 30°. 过点B'作B'E⊥BC于点E,则AB = B'E = $\frac{1}{2}$CB' = 2.
∴AD//BC.
∴∠CBB' = ∠AB'B = 75°. 由旋转的性质,得CB = CB',
∴∠CB'B = ∠CBB' = 75°.
∴∠BCB' = 180° - 75° - 75° = 30°,即旋转角α = 30°. 过点B'作B'E⊥BC于点E,则AB = B'E = $\frac{1}{2}$CB' = 2.
12. 如图,点E为正方形ABCD外一点,∠AEB =
90°,将Rt△ABE绕点A按逆时针方向旋转
90°得到△ADF,DF的延长线交BE于点H.
(1)试判断四边形AFHE的形状,并说明
理由;
(2)已知BH = 7,BC = 13,求DH的长.
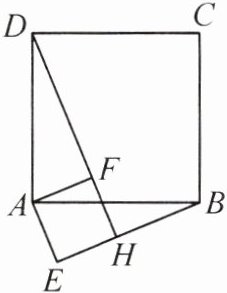
90°,将Rt△ABE绕点A按逆时针方向旋转
90°得到△ADF,DF的延长线交BE于点H.
(1)试判断四边形AFHE的形状,并说明
理由;
(2)已知BH = 7,BC = 13,求DH的长.

答案:
解:
(1)四边形AFHE是正方形,理由如下:
∵Rt△ABE绕点A按逆时针方向旋转90°得到△ADF,
∴Rt△ABE≌Rt△ADF.
∴∠BAE = ∠DAF,∠AEB = ∠AFD = 90°,AE = AF.
∴∠AFH = 90°. 又
∵∠DAF + ∠FAB = 90°,
∴∠BAE + ∠FAB = 90°.
∴∠FAE = 90°.
∴四边形AFHE是矩形. 又
∵AE = AF,
∴四边形AFHE是正方形.
(2)设AE = x.
∵四边形AFHE和四边形ABCD是正方形,
∴AE = EH = FH = x,BC = AB = 13. 在Rt△AEB中,AB² = AE² + BE²,又
∵BH = 7,
∴BE = x + 7.
∴13² = x² + (x + 7)²,解得x = 5.
∴BE = 5 + 7 = 12. 由旋转的性质,得DF = BE,
∴DH = DF + FH = 12 + 5 = 17.
(1)四边形AFHE是正方形,理由如下:
∵Rt△ABE绕点A按逆时针方向旋转90°得到△ADF,
∴Rt△ABE≌Rt△ADF.
∴∠BAE = ∠DAF,∠AEB = ∠AFD = 90°,AE = AF.
∴∠AFH = 90°. 又
∵∠DAF + ∠FAB = 90°,
∴∠BAE + ∠FAB = 90°.
∴∠FAE = 90°.
∴四边形AFHE是矩形. 又
∵AE = AF,
∴四边形AFHE是正方形.
(2)设AE = x.
∵四边形AFHE和四边形ABCD是正方形,
∴AE = EH = FH = x,BC = AB = 13. 在Rt△AEB中,AB² = AE² + BE²,又
∵BH = 7,
∴BE = x + 7.
∴13² = x² + (x + 7)²,解得x = 5.
∴BE = 5 + 7 = 12. 由旋转的性质,得DF = BE,
∴DH = DF + FH = 12 + 5 = 17.
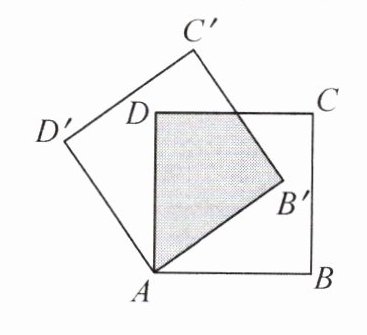
13. 如图,将正方形纸片ABCD绕着点A按逆
时针方向旋转30°后得到正方形AB'C'D'.
若AB = 2$\sqrt{3}$ cm,则图中阴影部分的面积为
( )
A. 6 cm²
B.(12 - 6$\sqrt{3}$)cm²
C. 3$\sqrt{3}$ cm²
D. 4$\sqrt{3}$ cm²
时针方向旋转30°后得到正方形AB'C'D'.
若AB = 2$\sqrt{3}$ cm,则图中阴影部分的面积为
( )

A. 6 cm²
B.(12 - 6$\sqrt{3}$)cm²
C. 3$\sqrt{3}$ cm²
D. 4$\sqrt{3}$ cm²
答案:
D
查看更多完整答案,请扫码查看


