《2025年名校课堂九年级数学下册沪科版安徽专版》

12. 已知$\odot O$是以坐标原点$O$为圆心，$5$为半径的圆，点$M$的坐标为$(-3,4)$，则点$M$与$\odot O$的位置关系为 （ ）
A. 点$M$在$\odot O$上
B. 点$M$在$\odot O$内
C. 点$M$在$\odot O$外
D. 点$M$在$\odot O$右上方

答案： A

13. 如图，$AB$是$\odot O$的直径，点$D$，$C$在$\odot O$上，$AD// OC$，$\angle DAB = 60^{\circ}$，连接$AC$，则$\angle DAC =$ （ ）


A. $15^{\circ}$
B. $30^{\circ}$
C. $45^{\circ}$
D. $60^{\circ}$

答案： B

14. 下列命题，其中正确的有 （ ）
①两个端点能够重合的弧是等弧；②面积相等的两个圆是等圆；③弦是圆上任意两点之间的部分；④同圆或等圆中，劣弧比优弧短。
A. $1$个
B. $2$个
C. $3$个
D. $4$个

答案： B

15. 如图，点$A$，$D$，$G$，$M$在半圆$O$上，四边形$ABOC$，$DEOF$，$HMNO$均为矩形。设$BC = a$，$EF = b$，$NH = c$，则下列各式中正确的是 （ ）

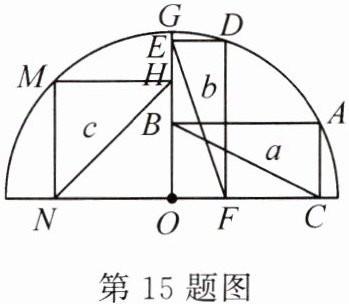
A. $a＞b＞c$
B. $b＞c＞a$
C. $c＞a＞b$
D. $a = b = c$

答案： D

16. 如图，数轴上半径为$1$的半圆$O$从原点开始以每秒$1$个单位长度的速度向右运动，同时，距原点右边$7$个单位长度有一点$P$以每秒$2$个单位长度的速度向左运动，经过 秒后，点$P$在$\odot O$上。

答案： 2或$\frac{8}{3}$

17. 如图所示，$AB$是$\odot O$的弦，半径$OC$，$OD$分别交$AB$于点$E$，$F$，且$AE = BF$，请写出线段$OE$与$OF$的数量关系，并给予证明。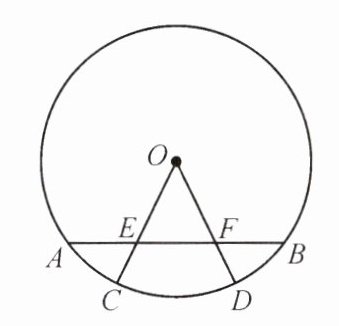

答案： 解：OE = OF. 证明：连接OA，OB.
∵OA，OB是⊙O的半径，
∴OA = OB.
∴∠OAB = ∠OBA. 又
∵AE = BF，
∴△OAE≌△OBF（SAS）.
∴OE = OF.

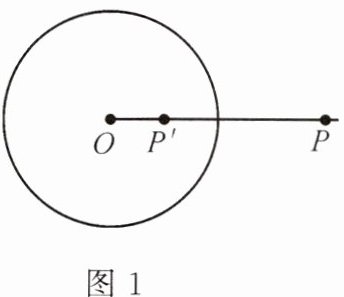
18. 【新定义问题】如图1，$\odot O$的半径为$r(r＞0)$，若点$P'$在射线$OP$上，满足$OP'\cdot OP = r^{2}$，则称点$P'$是点$P$关于$\odot O$的“反演点”。
如图2，$\odot O$的半径为$4$，点$B$在$\odot O$上，$\angle BOA = 60^{\circ}$，$OA = 8$。若点$A'$，$B'$分别是点$A$，$B$关于$\odot O$的反演点，求$A'B'$的长。

答案： 解：设OA交⊙O于点M，连接BM，B'A'.
∵OA'·OA = r²，r = 4，OA = 8，
∴OA' = 2.
∵OB'·OB = r²，r = 4，OB = 4，
∴OB' = 4，即点B和B'重合.
∵∠B'OA = 60°，OB' = OM，
∴△OB'M为等边三角形.
∵OA' = 2，OM = OB = 4，
∴A'为OM的中点.
∴B'A'⊥OM. 在Rt△OA'B'中，A'B' = $\sqrt{OB'^{2}-OA'^{2}}$ = $\sqrt{4^{2}-2^{2}}$ = 2$\sqrt{3}$.