《2025年名校课堂九年级数学下册沪科版安徽专版》

13. 如图，在正六边形 $ ABCDEF $ 中， $ AB = 2 $，点 $ P $ 是 $ ED $ 的中点，连接 $ AP $，则 $ AP $ 的长为（ ）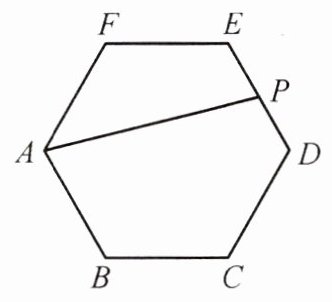
A. $ 2\sqrt{3} $
B. 4
C. $ \sqrt{13} $
D. $ \sqrt{11} $

答案： C

14.（2023·安徽）如图，正五边形 $ ABCDE $ 内接于 $ \odot O $，连接 $ OC $， $ OD $，则 $ \angle BAE-\angle COD = $（ ）

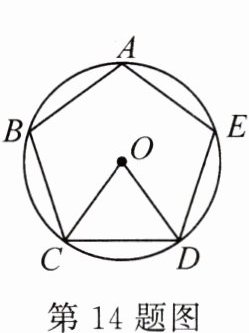
A. $ 60^{\circ} $
B. $ 54^{\circ} $
C. $ 48^{\circ} $
D. $ 36^{\circ} $

答案： D

15. 如图，正五边形 $ ABCDE $ 内接于 $ \odot O $，点 $ P $ 为 $ \overset{\frown}{DE} $ 上一点（点 $ P $ 与点 $ D $， $ E $ 不重合），连接 $ PC $， $ PD $， $ DG\perp PC $，垂足为 $ G $，则 $ \angle PDG $ 等于______度.

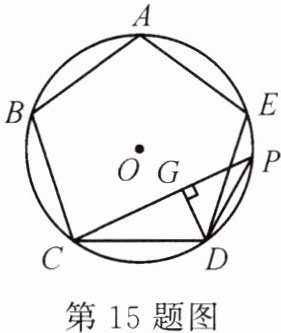
答案： 54

16. 如图，已知 $ \odot O $ 的两直径 $ AB $， $ CD $ 互相垂直，弦 $ MN $ 垂直平分 $ OB $，交 $ OB $ 于点 $ E $. 求证： $ MB $ 与 $ MC $ 分别为 $ \odot O $ 的内接正六边形和正十二边形的边长.

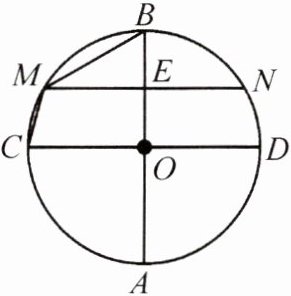
答案： 证明：连接$OM$。$\because MN$垂直平分$OB$，$\therefore MB = MO$。又$\because MO = OB$，$\therefore MO = OB = MB$，即$\triangle MOB$为等边三角形。$\therefore\angle MOB = 60^{\circ}$。$\therefore\angle MOC = 30^{\circ}$。$\because\angle MOB=\frac{360^{\circ}}{6}=60^{\circ}$，$\angle MOC=\frac{360^{\circ}}{12}=30^{\circ}$，$\therefore MB$，$MC$分别是$\odot O$内接正六边形和正十二边形的边长。

17. 如图，正五边形 $ ABCDE $ 的对角线 $ AC $， $ BE $ 相交于点 $ M $. 求证：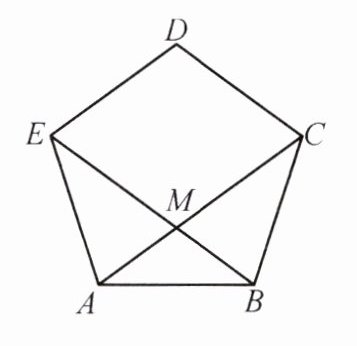
（1）四边形 $ CDEM $ 是菱形；
（2） $ M $ 是线段 $ BE $ 的黄金分割点.

答案： 证明：
(1)$\because$五边形$ABCDE$是正五边形，$\therefore DE = DC$，$\angle D=\angle DCB=\angle ABC = 108^{\circ}$，$\angle ACB=\frac{180^{\circ}-\angle ABC}{2}=36^{\circ}$，$\therefore\angle DCA = 72^{\circ}$。$\therefore\angle D+\angle DCA = 180^{\circ}$。$\therefore DE// AC$。同理可证$DC// BE$。$\therefore$四边形$DEMC$为平行四边形。又$\because DE = DC$，$\therefore$四边形$CDEM$是菱形。
(2)易证$\angle BAC=\angle AEB = 36^{\circ}$。$\because\angle ABM=\angle EBA$，$\therefore\triangle ABM\sim\triangle EBA$。$\therefore\frac{BM}{BA}=\frac{AB}{EB}$。$\therefore AB^{2}=BE\cdot BM$。由
(1)，得$\angle EAM = 72^{\circ}$，$\therefore\angle EMA = 180^{\circ}-36^{\circ}-72^{\circ}=72^{\circ}$。$\therefore ME = AE = AB$。$\therefore ME^{2}=BE\cdot BM$，即$M$是线段$BE$的黄金分割点。

18. 如图，有一个 $ \odot O $ 和两个正六边形 $ T_1 $， $ T_2 $. $ T_1 $ 的6个顶点都在圆周上， $ T_2 $ 的6条边都和 $ \odot O $ 相切（我们称 $ T_1 $， $ T_2 $ 分别为 $ \odot O $ 的内接正六边形和外切正六边形）. 若设 $ T_1 $， $ T_2 $ 的边长分别为 $ a $， $ b $， $ \odot O $ 的半径为 $ r $，则 $ r:a = $________； $ r:b = $________；正六边形 $ T_1 $， $ T_2 $ 的面积比 $ S_1:S_2 = $________.

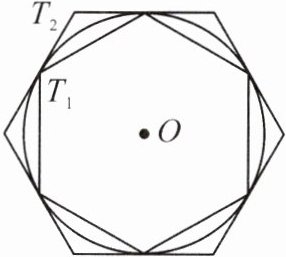
答案： $1:1$@@$\sqrt{3}:2$@@$3:4$