《2025年名校课堂九年级数学下册沪科版安徽专版》

1. 如图，边长为2的正六边形 $ ABCDEF $ 内接于 $ \odot O $，则该正六边形的边心距为（ ）

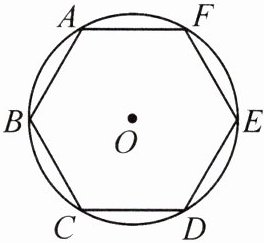
A. 1
B. 2
C. $ \sqrt{3} $
D. $ 2\sqrt{3} $

答案： C

2.（2024·合肥瑶海区一模）如图，正五边形 $ ABCDE $ 内接于 $ \odot O $，则 $ \angle CAB $ 的度数是（ ）

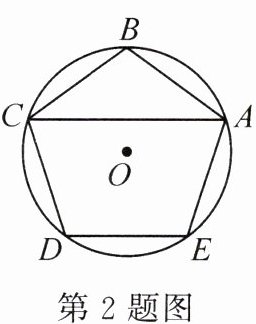
A. $ 26^{\circ} $
B. $ 30^{\circ} $
C. $ 36^{\circ} $
D. $ 45^{\circ} $

答案： C

3. 如图，螺母的外围可以看作是正六边形 $ ABCDEF $，已知这个正六边形的半径是2，则它的周长是（ ）

A. $ 6\sqrt{3} $
B. $ 12\sqrt{3} $
C. 12
D. 24

答案： C

4. 若正方形的外接圆半径为2，则其内切圆半径为（ ）
A. $ \sqrt{2} $
B. $ 2\sqrt{2} $
C. $ \frac{\sqrt{2}}{2} $
D. 1

答案： A

5. 已知 $ \odot O $ 的面积为 $ 4\pi $，则其内接正三角形的面积为（ ）
A. $ 3\sqrt{3} $
B. $ 3\sqrt{6} $
C. $ \frac{3}{2}\sqrt{3} $
D. $ \frac{3}{2}\sqrt{6} $

答案： A

6.（2023·合肥蜀山区期末）如图，正五边形 $ ABCDE $ 内接于 $ \odot O $，点 $ F $ 在弧 $ AE $ 上. 若 $ \angle FCD = 70^{\circ} $，则 $ \angle FDC $ 度数为（ ）

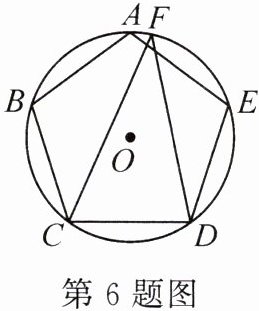
A. $ 64^{\circ} $
B. $ 72^{\circ} $
C. $ 74^{\circ} $
D. $ 80^{\circ} $

答案： C

7. 已知圆的半径是6，则圆内接正三角形的边长是________.

答案： $6\sqrt{3}$

8. 同一个圆的内接正方形和内接正三角形的边心距的比为________.

答案： $\sqrt{2}:1$

9. 如图所示的向日葵图案是用等分圆周画出的，则 $ \odot O $ 与半圆 $ P $ 的半径比为________.

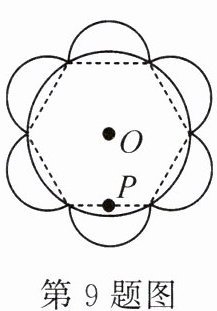
答案： $2:1$

10.（教材P51例题变式）求边长为20 cm的正六边形的面积与此正六边形内切圆周长和外接圆面积.

答案：
解：如图，易知$\angle AOB=\frac{360^{\circ}}{6}=60^{\circ}$，$\therefore\angle DOB = 30^{\circ}$。又$\because AB = 20\ cm$，$\therefore DB = 10\ cm$。在$Rt\triangle OBD$中，可求得$OD = 10\sqrt{3}\ cm$，$OB = 20\ cm$。$\therefore S_{正六边形}=6S_{\triangle OAB}=6\times\frac{1}{2}\times20\times10\sqrt{3}=600\sqrt{3}(cm^{2})$。正六边形内切圆周长为$2\pi\cdot OD = 20\sqrt{3}\pi\ cm$。正六边形外接圆面积为$\pi\cdot OB^{2}=400\pi\ cm^{2}$。 

11. 正五边形绕其中心旋转下列各角度，所得正五边形与原正五边形不重合的是（ ）
A. $ 216^{\circ} $
B. $ 144^{\circ} $
C. $ 120^{\circ} $
D. $ 72^{\circ} $

答案： C

12. 正二十边形的对称轴有______条.

答案： 20