第83页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
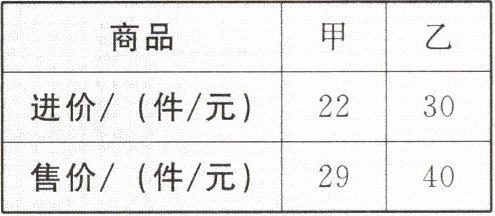
【例4】 某超市第一次用5560元购进甲、乙两种商品,其中乙种商品的件数比甲种商品件数的$\frac{1}{2}$少12件,甲、乙两种商品的进价和零售价如下表(注:利润 = 售价 - 进价):
|商品|甲|乙|
|进价/(件/元)|22|30|
|售价/(件/元)|29|40|
(1)第一次进货时甲、乙两种商品各购进多少件?
(2)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的2倍,甲种商品按原价销售,乙种商品打折销售。第二次两种商品都销售完后盈利1392元,求第二次乙种商品是按原价打几折销售的。
(1)解:设第一次甲种商品购进$x$件。
根据“甲的进货钱数 + 乙的进货钱数 = 总钱数”,
列得方程$22x + 30(\frac{1}{2}x - 12) = 5560$。
解得$x = 160$。
则$\frac{1}{2}x - 12 = \frac{1}{2}×160 - 12 = 68$。
答:第一次甲、乙两种商品分别购进160件和68件。
(2)设第二次乙种商品按打$y$折销售。
根据“甲商品盈利 + 乙商品打折后盈利 = 总盈利”,
列得方程$160×(29 - 22) + 68×2×(40×\frac{y}{10} - 30) = 1392$。
解得$y = 8$。
答:第二次乙种商品是按原价打八折销售的。
|商品|甲|乙|
|进价/(件/元)|22|30|
|售价/(件/元)|29|40|

(1)第一次进货时甲、乙两种商品各购进多少件?
(2)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的2倍,甲种商品按原价销售,乙种商品打折销售。第二次两种商品都销售完后盈利1392元,求第二次乙种商品是按原价打几折销售的。
(1)解:设第一次甲种商品购进$x$件。
根据“甲的进货钱数 + 乙的进货钱数 = 总钱数”,
列得方程$22x + 30(\frac{1}{2}x - 12) = 5560$。
解得$x = 160$。
则$\frac{1}{2}x - 12 = \frac{1}{2}×160 - 12 = 68$。
答:第一次甲、乙两种商品分别购进160件和68件。
(2)设第二次乙种商品按打$y$折销售。
根据“甲商品盈利 + 乙商品打折后盈利 = 总盈利”,
列得方程$160×(29 - 22) + 68×2×(40×\frac{y}{10} - 30) = 1392$。
解得$y = 8$。
答:第二次乙种商品是按原价打八折销售的。
答案:
(1)设第一次甲种商品购进$x$件,则乙种商品购进$(\frac{1}{2}x - 12)$件。
由进价可得方程:
$22x + 30(\frac{1}{2}x - 12) = 5560$,
$22x + 15x - 360 = 5560$,
$37x = 5920$,
$x = 160$。
则$\frac{1}{2}x - 12 = \frac{1}{2} × 160 - 12 = 68$。
答:第一次甲、乙两种商品分别购进160件和68件。
(2)设第二次乙种商品按打$y$折销售。
甲商品盈利:$160 × (29 - 22) = 1120$(元),
乙商品打折后盈利:$68 × 2 × (40 × \frac{y}{10} - 30)$,
由总盈利可得方程:
$1120 + 68 × 2 × (40 × \frac{y}{10} - 30) = 1392$,
$1120 + 136 × (4y - 30) = 1392$,
$136 × (4y - 30) = 272$,
$4y - 30 = 2$,
$4y = 32$,
$y = 8$。
答:第二次乙种商品是按原价打八折销售的。
(1)设第一次甲种商品购进$x$件,则乙种商品购进$(\frac{1}{2}x - 12)$件。
由进价可得方程:
$22x + 30(\frac{1}{2}x - 12) = 5560$,
$22x + 15x - 360 = 5560$,
$37x = 5920$,
$x = 160$。
则$\frac{1}{2}x - 12 = \frac{1}{2} × 160 - 12 = 68$。
答:第一次甲、乙两种商品分别购进160件和68件。
(2)设第二次乙种商品按打$y$折销售。
甲商品盈利:$160 × (29 - 22) = 1120$(元),
乙商品打折后盈利:$68 × 2 × (40 × \frac{y}{10} - 30)$,
由总盈利可得方程:
$1120 + 68 × 2 × (40 × \frac{y}{10} - 30) = 1392$,
$1120 + 136 × (4y - 30) = 1392$,
$136 × (4y - 30) = 272$,
$4y - 30 = 2$,
$4y = 32$,
$y = 8$。
答:第二次乙种商品是按原价打八折销售的。
3. 某次“垃圾分类”活动共有120名学生参与,将学生分成宣传组和劳动组,并要求宣传组人数是劳动组人数的一半。小马同学利用一元一次方程解决这个问题,设宣传组有$x$人,依题意列式为$\frac{x}{120} = $_________$$,将方程补全完整,横线处应填( )。
A.$\frac{1}{2}$
B.$\frac{1}{1 + 2}$
C.$\frac{2}{1 + \frac{1}{2}}$
D.$\frac{2}{1 + 2}$
A.$\frac{1}{2}$
B.$\frac{1}{1 + 2}$
C.$\frac{2}{1 + \frac{1}{2}}$
D.$\frac{2}{1 + 2}$
答案:
B
4. 小红同学乘坐出租车从学校回家看望爷爷,出租车的收费标准是:起步价5元(含3km),超过3km的按每千米1.2元收费,下车后,小红付车费37.4元,求小红从乘车点到家的距离。
答案:
解:设小红从乘车点到家的距离是x km.根据题意,列得方程5+1.2(x-3)=37.4.解得x=30.答:小红从乘车点到家的距离是30 km.
查看更多完整答案,请扫码查看


