《2025年家庭作业七年级数学上册人教版》

【例2】先观察下列各式,再回答问题：
①$1×3 - 2^{2} = 3 - 4 = -1$；
②$2×4 - 3^{2} = 8 - 9 = -1$；
③$3×5 - 4^{2} = 15 - 16 = -1$；
……
(1)请按以上规律写出第$4$个算式：______；
(2)用含$n的代数式表示出第n$个算式：______。
解析：每一个式子中最左边的数跟序号相同,第$2个数比第1个数大2$,第$3个数是比第1个数大1$的数的平方,最后结果均为$-1$。由此,不难得出第$4个算式应该为4×6 - 5^{2} = 24 - 25 = -1$,第$n个算式应该为n(n + 2) - (n + 1)^{2} = -1$。
答案：(1)$4×6 - 5^{2} = 24 - 25 = -1$ (2)$n(n + 2) - (n + 1)^{2} = -1$

答案：
(1)4×6 - 5²=24 - 25=-1；
(2)n(n+2)-(n+1)²=-1

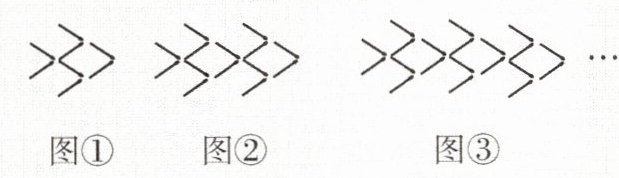
1. 如图,下面是用火柴棒摆出的“金鱼”,按照下图的规律,摆第$n$个图需要的火柴棒的根数为( )。
……

A.$6n + 2$
B.$6n + 8$
C.$8n$
D.$4n + 4$

答案： A

2. 一组等式：$1^{2} + 2^{2} + 2^{2} = 3^{2}$,$2^{2} + 3^{2} + 6^{2} = 7^{2}$,$3^{2} + 4^{2} + 12^{2} = 13^{2}$,$4^{2} + 5^{2} + 20^{2} = 21^{2}$,……请观察它们的构成规律,用你发现的规律写出第$n$个等式：______。

答案： $n^{2}+(n+1)^{2}+[n(n+1)]^{2}=[n(n+1)+1]^{2}$

【例3】已知$a = 3$,$b = -4$,求代数式$a^{2} - b^{2} + 3a - b$的值。
解：当$a = 3$,$b = -4$时,$a^{2} - b^{2} + 3a - b = 3^{2} - (-4)^{2} + 3×3 - (-4) = 9 - 16 + 9 + 4 = 6$。

答案： $6$

【例4】已知$x + y = 2025$,$xy = 2024$,求$xy - 2(x + y)$的值。
解：当$x + y = 2025$,$xy = 2024$时,$xy - 2(x + y) = 2024 - 2×2025 = -2026$。

答案： 答题卡：
由题意知 $x + y = 2025$，$xy = 2024$，
代入 $xy - 2(x + y)$，
得：
$xy - 2(x + y) $
$= 2024 - 2 × 2025 $
$= 2024 - 4050$
$ = -2026$
所以$xy - 2(x + y)$的值为$-2026$。

3. 若$x = 2$,$y = -6$,则$y^{2} + 2x - 6$的值是______。

答案： 34

4. 已知$x + 2y = 3$,则$7 + 2x + 4y = $______。

答案： 13