《2025年家庭作业七年级数学上册人教版》

3. 将下列各数填入相应的集合内：
-12,$-\frac{2}{3}$,18,$-0.\dot{4}$,0,$3\frac{1}{4}$,0.63,π,92,-7.
(1)正有理数集合：…{ }.
(2)正整数集合：…{ }.
(3)负有理数集合：…{ }.

答案： （1）18，$3\frac{1}{4}$，0.63，92， （2）18，92， （3）-12，$-\frac{2}{3}$，$-0.\dot{4}$，-7，

4. 有一次同学聚会,小王的座位号与下列各数中的负有理数的个数相等；小李的座位号与下列各数中的正整数的个数相等.
6,$-7\frac{1}{3}$,0,-200,$+4\frac{1}{3}$,$-3.\dot{2}$,-0.68,+67,$-\frac{3}{7}$,-10%,999,-24.
(1)小王、小李坐的各是第几号位置？
(2)若这次同学聚会的人数是小王的座位号的 2 倍与小李的座位号的 4 倍的和,则这次聚会到了多少名同学？

答案： 解：（1）在这个数组中，负有理数有$-7\frac{1}{3}$，-200，$-3.\dot{2}$，-0.68，$-\frac{3}{7}$，-10%，-24，共7个，所以小王坐的是第7号位置；正整数有6，+67，999，共3个，所以小李坐的是第3号位置.（2）$7×2+3×4=26$（名）. 所以这次聚会到了26名同学.

5. 如图,将一串数按下列规律排列,回答下列问题：

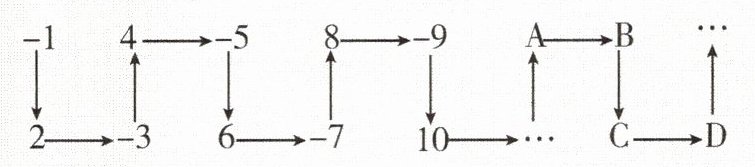
(1)在 A 处的数是____(填“正有理数”“负有理数”或“0”)；
(2)负有理数排在 A,B,C,D 中的什么位置？
(3)第 2024 个数是正有理数还是负有理数？排在 A,B,C,D 中的什么位置？

答案： 解：（1）正有理数（2）负有理数排在B和D的位置.（3）观察可知，奇数为负，偶数为正，所以第2024个数是正有理数.从头开始把4个数字看成一组，$2024÷4=506$，所以第2024个数排在A的位置.

1. 规定了____、____和____的直线叫作数轴.

答案： 原点 正方向 单位长度

2. ____将数轴(____除外)分成两部分,其中____一侧的部分叫作数轴的正半轴；另一侧的部分叫作数轴的____.

答案： 原点 原点 正方向 负半轴