第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
1. 有理数减法法则
减去一个数,等于加这个数的____.
减去一个数,等于加这个数的____.
答案:
相反数
2. 有理数减法法则也可以表示成:$a - b = a + ($____$)$.
答案:
-b
【例1】计算:
(1)$2 - (-3)$;
(2)$\frac{2}{3} - (+ \frac{1}{6})$;
(3)$(-5 \frac{2}{3}) - \frac{1}{3}$;
(4)$0 - (-6.2)$.
解:(1)$2 - (-3) = 2 + 3 = 5$;
(2)$\frac{2}{3} - (+ \frac{1}{6}) = \frac{2}{3} + (- \frac{1}{6}) = \frac{1}{2}$;
(3)$(-5 \frac{2}{3}) - \frac{1}{3} = (-5 \frac{2}{3}) + (- \frac{1}{3}) = -6$;
(4)$0 - (-6.2) = 0 + 6.2 = 6.2$.
(1)$2 - (-3)$;
(2)$\frac{2}{3} - (+ \frac{1}{6})$;
(3)$(-5 \frac{2}{3}) - \frac{1}{3}$;
(4)$0 - (-6.2)$.
解:(1)$2 - (-3) = 2 + 3 = 5$;
(2)$\frac{2}{3} - (+ \frac{1}{6}) = \frac{2}{3} + (- \frac{1}{6}) = \frac{1}{2}$;
(3)$(-5 \frac{2}{3}) - \frac{1}{3} = (-5 \frac{2}{3}) + (- \frac{1}{3}) = -6$;
(4)$0 - (-6.2) = 0 + 6.2 = 6.2$.
答案:
(1)
$2 - (-3)$
$= 2 + 3$
$= 5$
(2)
$\frac{2}{3} - (+\frac{1}{6})$
$=\frac{2}{3} + (-\frac{1}{6})$
$=\frac{4}{6} - \frac{1}{6}$
$=\frac{3}{6}$
$=\frac{1}{2}$
(3)
$(-5\frac{2}{3}) - \frac{1}{3}$
$= (-5\frac{2}{3}) + (-\frac{1}{3})$
$=-(5\frac{2}{3} + \frac{1}{3})$
$=-6$
(4)
$0 - (-6.2)$
$= 0 + 6.2$
$= 6.2$
(1)
$2 - (-3)$
$= 2 + 3$
$= 5$
(2)
$\frac{2}{3} - (+\frac{1}{6})$
$=\frac{2}{3} + (-\frac{1}{6})$
$=\frac{4}{6} - \frac{1}{6}$
$=\frac{3}{6}$
$=\frac{1}{2}$
(3)
$(-5\frac{2}{3}) - \frac{1}{3}$
$= (-5\frac{2}{3}) + (-\frac{1}{3})$
$=-(5\frac{2}{3} + \frac{1}{3})$
$=-6$
(4)
$0 - (-6.2)$
$= 0 + 6.2$
$= 6.2$
1. 下列计算正确的是( ).
A.$(-14) - (+5) = -9$
B.$0 - (-3) = 3$
C.$(-3) - (-3) = -6$
D.$5 - (-3) = 2$
A.$(-14) - (+5) = -9$
B.$0 - (-3) = 3$
C.$(-3) - (-3) = -6$
D.$5 - (-3) = 2$
答案:
B
【例2】计算:
$-0.5 + (- \frac{1}{4}) - (+2.75) + \frac{1}{2}$.
解:原式$= - \frac{1}{2} + (- \frac{1}{4}) + (-2 \frac{3}{4}) + \frac{1}{2} = (- \frac{1}{2} + \frac{1}{2}) + [(- \frac{1}{4}) + (-2 \frac{3}{4})] = 0 + (-3) = -3$.
$-0.5 + (- \frac{1}{4}) - (+2.75) + \frac{1}{2}$.
解:原式$= - \frac{1}{2} + (- \frac{1}{4}) + (-2 \frac{3}{4}) + \frac{1}{2} = (- \frac{1}{2} + \frac{1}{2}) + [(- \frac{1}{4}) + (-2 \frac{3}{4})] = 0 + (-3) = -3$.
答案:
解:原式$=-\frac{1}{2}+\left(-\frac{1}{4}\right)+\left(-2\frac{3}{4}\right)+\frac{1}{2}$
$=\left(-\frac{1}{2}+\frac{1}{2}\right)+\left[\left(-\frac{1}{4}\right)+\left(-2\frac{3}{4}\right)\right]$
$=0+\left(-3\right)$
$=-3$
$=\left(-\frac{1}{2}+\frac{1}{2}\right)+\left[\left(-\frac{1}{4}\right)+\left(-2\frac{3}{4}\right)\right]$
$=0+\left(-3\right)$
$=-3$
2. 若“方框”$\begin{array}{|cc|} x & w \\ y & z \end{array} 表示运算x - y + z + w$,则“方框”$\begin{array}{|cc|} -2 & 3 \\ 3 & -6 \end{array} 的运算结果是= $____.
答案:
-8
【例3】如图,在数轴上有四个点$A$,$B$,$C$,$D$.
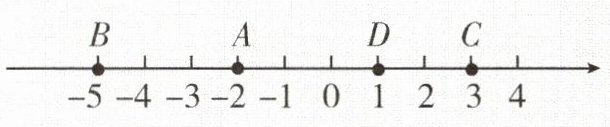
请根据图中的信息,回答下列问题:
(1)$A$,$C$两点之间的距离是多少?
(2)$B$,$D$两点之间的距离是多少?
解:(1)观察数轴,可知点$A$,点$C表示的数分别为-2$,$3$,所以它们之间的距离为$\vert 3 - (-2) \vert = 5$.
(2)观察数轴,可知点$B$,点$D表示的数分别为-5$,$1$,所以它们之间的距离为$\vert 1 - (-5) \vert = 6$.
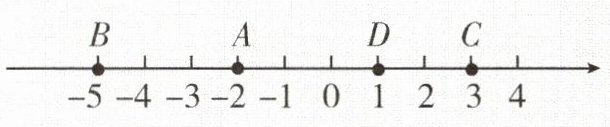
请根据图中的信息,回答下列问题:
(1)$A$,$C$两点之间的距离是多少?
(2)$B$,$D$两点之间的距离是多少?
解:(1)观察数轴,可知点$A$,点$C表示的数分别为-2$,$3$,所以它们之间的距离为$\vert 3 - (-2) \vert = 5$.
(2)观察数轴,可知点$B$,点$D表示的数分别为-5$,$1$,所以它们之间的距离为$\vert 1 - (-5) \vert = 6$.
答案:
(1) 点 $A$ 表示的数为 $-2$,点 $C$ 表示的数为 $3$,
两点之间的距离为:
$\vert 3 - (-2) \vert = 5$
(2) 点 $B$ 表示的数为 $-5$,点 $D$ 表示的数为 $1$,
两点之间的距离为:
$\vert 1 - (-5) \vert = 6$
(1) 点 $A$ 表示的数为 $-2$,点 $C$ 表示的数为 $3$,
两点之间的距离为:
$\vert 3 - (-2) \vert = 5$
(2) 点 $B$ 表示的数为 $-5$,点 $D$ 表示的数为 $1$,
两点之间的距离为:
$\vert 1 - (-5) \vert = 6$
查看更多完整答案,请扫码查看


