《2025年家庭作业七年级数学上册人教版》

一般地,用______代替代数式中的______,按照代数式中的______关系计算得出的结果,叫作代数式的值. 当字母取不同的数值时,代数式的值一般也不同.

答案： 数值 字母 运算

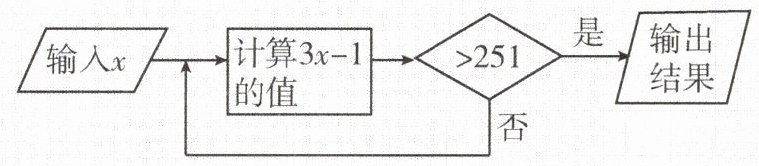
【例】一个运算程序如图所示,若输入 $ x $ 的值是 38,则输出结果是( ).


A.337
B.338
C.339
D.340
解析：先代入 38 计算,再判断是否能输出. 若不能输出,则再次代入计算. 当输入 38 时,$ 3x - 1 = 3×38 - 1 = 113 $. 因为 $ 113 ＜ 251 $,所以需再次输入,$ 3x - 1 = 3×113 - 1 = 339 - 1 = 338 $. $ 338 ＞ 251 $,所以输出 338.
答案：B

答案： B

1. 根据下面给出的 $ a $,$ b $ 的值,求代数式 $ b^{2} - 4ac $ 的值.
(1)$ a = 2 $,$ b = - 3 $,$ c = - 4 $；
(2)$ a = 9 $,$ b = 6 $,$ c = 1 $.

答案： 解：（1）当a=2，b=-3，c=-4时，b²-4ac=(-3)²-4×2×(-4)=9+32=41；
（2）当a=9，b=6，c=1时，b²-4ac=6²-4×9×1=36-36=0.

2. 如图,一个花坛由两个半圆和一个长方形组成,已知半圆的半径为 $ R $(单位：m),长方形的长为 $ a $(单位：m).

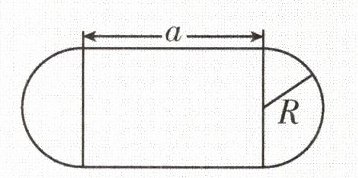
(1)求花坛的面积(用代数式表示)；
(2)当 $ R = 2.5m $,$ a = 10m $ 时,计算花坛的面积($ \pi $ 取 3).

答案： 解：（1）由题意，得花坛面积是（2aR+πR²）m².
（2）当R=2.5 m，a=10 m时，2aR+πR²=2×10×2.5+3×2.5²=68.75（m²）.
答：当R=2.5 m，a=10 m时，花坛的面积是68.75 m².