第29页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
1. 有理数除法法则
除以一个不等于 0 的数,等于乘这个数的______.
这个法则也可以表示成 $ a ÷ b = a \cdot $______$(b \neq 0)$.
除以一个不等于 0 的数,等于乘这个数的______.
这个法则也可以表示成 $ a ÷ b = a \cdot $______$(b \neq 0)$.
答案:
倒数 $\frac{1}{b}$
2. 从有理数除法法则,容易得出:
(1) 两数相除,同号得______,异号得负,且商的绝对值等于被除数的绝对值除以______的绝对值的商;
(2) 0 除以任何一个不等于 0 的数,都得______.
(1) 两数相除,同号得______,异号得负,且商的绝对值等于被除数的绝对值除以______的绝对值的商;
(2) 0 除以任何一个不等于 0 的数,都得______.
答案:
(1)正 除数 (2)0
3. 有理数的加、减、乘、除混合运算,如无括号指出先做什么运算,则按照“先乘除,后______”的顺序进行.
答案:
加减
【例 1】计算:
(1) $(-15) ÷ (-3)$;
(2) $2\frac{1}{3} ÷ (-1\frac{1}{6})$.
解:
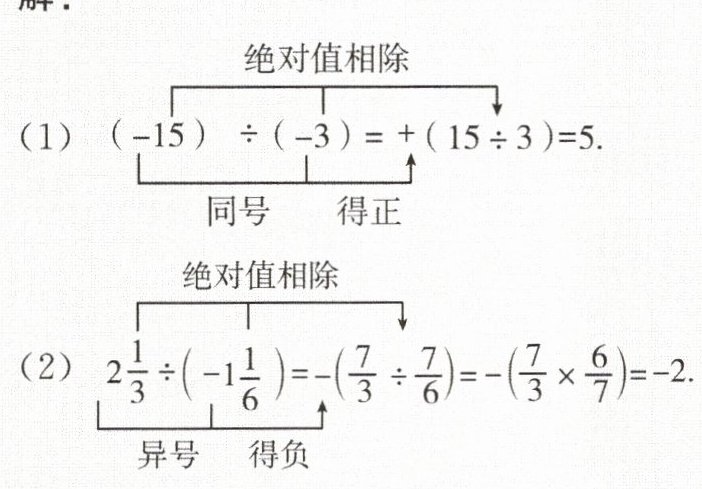
(1) $(-15) ÷ (-3) = +(15 ÷ 3) = 5$.
(2) $2\frac{1}{3} ÷ (-1\frac{1}{6}) = -(\frac{7}{3} ÷ \frac{7}{6}) = -(\frac{7}{3} × \frac{6}{7}) = -2$.
(1) $(-15) ÷ (-3)$;
(2) $2\frac{1}{3} ÷ (-1\frac{1}{6})$.
解:

(1) $(-15) ÷ (-3) = +(15 ÷ 3) = 5$.
(2) $2\frac{1}{3} ÷ (-1\frac{1}{6}) = -(\frac{7}{3} ÷ \frac{7}{6}) = -(\frac{7}{3} × \frac{6}{7}) = -2$.
答案:
(1) $(-15) ÷ (-3) = +(15 ÷ 3) = 5$;
(2) $2\frac{1}{3} ÷ (-1\frac{1}{6}) = -\left(\frac{7}{3} ÷ \frac{7}{6}\right) = -\left(\frac{7}{3} × \frac{6}{7}\right) = -2$.
(1) $(-15) ÷ (-3) = +(15 ÷ 3) = 5$;
(2) $2\frac{1}{3} ÷ (-1\frac{1}{6}) = -\left(\frac{7}{3} ÷ \frac{7}{6}\right) = -\left(\frac{7}{3} × \frac{6}{7}\right) = -2$.
1. 定义一种新运算“$\otimes$”,规则:$m \otimes n = (-\frac{1}{m}) ÷ \frac{n}{2}$. 例如:$2 \otimes 3 = (-\frac{1}{2}) ÷ \frac{3}{2} = -\frac{1}{2} × \frac{2}{3} = -\frac{1}{3}$.
计算下列各题:
(1) $(-2) \otimes 4$;
(2) $(-1) \otimes [(-5) \otimes 2]$.
计算下列各题:
(1) $(-2) \otimes 4$;
(2) $(-1) \otimes [(-5) \otimes 2]$.
答案:
解:(1)$(-2)\otimes4=-\frac{1}{-2}÷\frac{4}{2}=\frac{1}{2}×\frac{1}{2}=\frac{1}{4}$;
(2)$(-1)\otimes[(-5)\otimes2]=(-1)\otimes\left[-\frac{1}{-5}÷\frac{2}{2}\right]=(-1)\otimes\frac{1}{5}=-\frac{1}{-1}÷\frac{\frac{1}{5}}{2}=1×10=10$.
(2)$(-1)\otimes[(-5)\otimes2]=(-1)\otimes\left[-\frac{1}{-5}÷\frac{2}{2}\right]=(-1)\otimes\frac{1}{5}=-\frac{1}{-1}÷\frac{\frac{1}{5}}{2}=1×10=10$.
【例 2】化简:
(1) $\frac{-54}{-8}$;(2) $-\frac{-12}{-0.3}$.
解:(1) $\frac{-54}{-8} = (-54) ÷ (-8) = 54 ÷ 8 = \frac{27}{4}$;
(2) $-\frac{-12}{-0.3} = (-12) ÷ 0.3 = -40$.
(1) $\frac{-54}{-8}$;(2) $-\frac{-12}{-0.3}$.
解:(1) $\frac{-54}{-8} = (-54) ÷ (-8) = 54 ÷ 8 = \frac{27}{4}$;
(2) $-\frac{-12}{-0.3} = (-12) ÷ 0.3 = -40$.
答案:
(1)
$\frac{-54}{-8}$
$ = (-54)÷(-8)$
$ = 54÷8$
$=\frac{54}{8}$
$ = \frac{27}{4}$
(2)
$- \frac{-12}{-0.3}$
$=-((-12)÷(-0.3))$
$=-(12÷0.3)$
$ = - 40$
(1)
$\frac{-54}{-8}$
$ = (-54)÷(-8)$
$ = 54÷8$
$=\frac{54}{8}$
$ = \frac{27}{4}$
(2)
$- \frac{-12}{-0.3}$
$=-((-12)÷(-0.3))$
$=-(12÷0.3)$
$ = - 40$
2. 下列式子:① $\frac{0.3}{-\frac{1}{2}} = \frac{3}{5}$;② $\frac{-2}{-6} = \frac{1}{3}$;③ $\frac{-0.5}{-0.25} = 2$;④ $\frac{7}{-63} = \frac{1}{9}$.
其中正确的有( ).
A.1 个
B.2 个
C.3 个
D.4 个
其中正确的有( ).
A.1 个
B.2 个
C.3 个
D.4 个
答案:
B
查看更多完整答案,请扫码查看


