2025年金学典同步解析与测评贵州人民出版社九年级数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金学典同步解析与测评贵州人民出版社九年级数学上册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 下列方程中,一定是关于 $ x $ 的一元二次方程的是(
A.$ ax^{2}+bx+c= 0 $
B.$ x^{2}-5= 0 $
C.$ \frac{1}{x^{2}}+\frac{1}{x}= 6 $
D.$ x^{2}= x(x - 2)+1 $
B
).A.$ ax^{2}+bx+c= 0 $
B.$ x^{2}-5= 0 $
C.$ \frac{1}{x^{2}}+\frac{1}{x}= 6 $
D.$ x^{2}= x(x - 2)+1 $
答案:
B
2. 用配方法解方程 $ x^{2}+10x+9= 0 $,配方后可得(
A.$ (x + 5)^{2}= 16 $
B.$ (x + 5)^{2}= 1 $
C.$ (x + 10)^{2}= 91 $
D.$ (x + 10)^{2}= 109 $
A
).A.$ (x + 5)^{2}= 16 $
B.$ (x + 5)^{2}= 1 $
C.$ (x + 10)^{2}= 91 $
D.$ (x + 10)^{2}= 109 $
答案:
A
3. 一元二次方程 $ (x - 2)^{2}= x - 2 $ 的根是(
A.$ x = 2 $
B.$ x_{1}= 1,x_{2}= 3 $
C.$ x = 3 $
D.$ x_{1}= 2,x_{2}= 3 $
D
).A.$ x = 2 $
B.$ x_{1}= 1,x_{2}= 3 $
C.$ x = 3 $
D.$ x_{1}= 2,x_{2}= 3 $
答案:
D
4. 若关于 $ x $ 的一元二次方程 $ (k - 2)x^{2}+2x+3= 0 $ 有两个实数根,则 $ k $ 的取值范围是(
A.$ k\leqslant\frac{7}{3} $
B.$ k>\frac{7}{3} $
C.$ k<\frac{7}{3} $且 $ k\neq2 $
D.$ k\leqslant\frac{7}{3} $且 $ k\neq2 $
D
).A.$ k\leqslant\frac{7}{3} $
B.$ k>\frac{7}{3} $
C.$ k<\frac{7}{3} $且 $ k\neq2 $
D.$ k\leqslant\frac{7}{3} $且 $ k\neq2 $
答案:
D
5. 某专卖店一特产第三季度的总销量为 9.93 万件,其中 7 月份的销量为 3 万件,设 8,9 月份销量的月平均增长率为 $ x $,则可列方程为(
A.$ 3(1 + x)^{2}= 9.93 $
B.$ 3+3(1 + x)+3(1 + x)^{2}= 9.93 $
C.$ 3+3x+3(1 + x)^{2}= 9.93 $
D.$ 3+3(1 + x)^{2}= 9.93 $
B
).A.$ 3(1 + x)^{2}= 9.93 $
B.$ 3+3(1 + x)+3(1 + x)^{2}= 9.93 $
C.$ 3+3x+3(1 + x)^{2}= 9.93 $
D.$ 3+3(1 + x)^{2}= 9.93 $
答案:
B
6. 如图,在一个宽为 9 m,长为 16 m 的矩形地面上修等宽的三条互相垂直的小路,余下部分种草,草地面积为 112 $ m^{2} $. 设小路的宽为 $ x $ m,那么 $ x $ 满足的方程是(
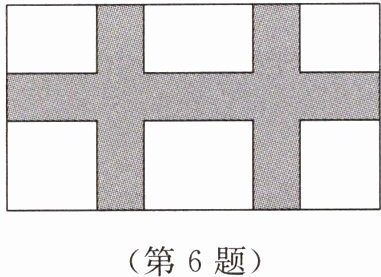
A.$ (9 - 2x)(16 - 2x)= 112 $
B.$ (9 - x)(16 - 2x)= 112 $
C.$ (9 - x)(16 - x)= 112 $
D.$ (9 - 2x)(16 - x)= 112 $
B
).
A.$ (9 - 2x)(16 - 2x)= 112 $
B.$ (9 - x)(16 - 2x)= 112 $
C.$ (9 - x)(16 - x)= 112 $
D.$ (9 - 2x)(16 - x)= 112 $
答案:
B
7. 如图,在 $ Rt\triangle ABC $ 中,$ \angle C = 90^{\circ},AC = 12 cm,BC = 16 cm $,点 $ P,Q $ 分别从 $ A,B $ 两点同时出发沿 $ AC,BC $ 方向向点 $ C $ 匀速运动,其速度均为 2 cm/s,当点 $ P $ 到达点 $ C $ 后,$ P,Q $ 两点均停止运动. 设运动时间为 $ t $ s,则当 $ \triangle PCQ $ 的面积是 $ \triangle ABC $ 的面积的一半时,$ t $ 的值为(
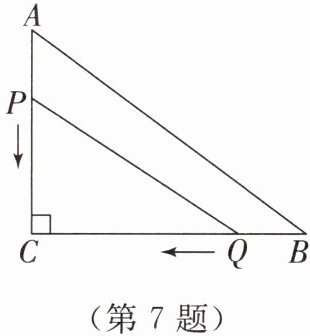
A.1
B.2
C.12
D.2 或 12
B
).
A.1
B.2
C.12
D.2 或 12
答案:
B
8. 若关于 $ x $ 的方程 $ (m - 1)x^{m^{2}+1}+4x - 2= 0 $ 是一元二次方程,则 $ m $ 的值为
-1
.
答案:
-1
9. 若关于 $ x $ 的方程 $ x^{2}-kx - 12= 0 $ 的一个根为 3,则 $ k $ 的值为
-1
.
答案:
-1
10. 如果 $ m $ 是方程 $ x^{2}-x + 1= 0 $ 的一个根,那么代数式 $ m(m - 1) $ 的值为
-1
.
答案:
-1
查看更多完整答案,请扫码查看


