《2025年金学典同步解析与测评贵州人民出版社九年级数学上册人教版》

某小区的圆柱形供水管道损坏,现在工人师傅要更换管道。如图24.1-2,工人师傅测量出管道有积水部分的最大深度是2 cm,水面的宽度为8 cm,他左思右想也不知道该用多粗的管道来替换,你能帮他解决这个问题吗？

答案： 【解析】：设管道横截面圆的圆心为O，半径为r cm。水面AB=8cm，过O作OC⊥AB于C，由垂径定理得AC=BC=4cm。设OC=d cm，积水最大深度CD=2cm（D为OC延长线与劣弧AB的交点），则OD=r，且OD=OC+CD，即r=d+2，故d=r-2。在Rt△OAC中，OA²=OC²+AC²，即r²=(r-2)²+4²。解得r=5，直径为10cm。
【答案】：10cm

1. 圆的对称性：圆是轴对称图形,任何一条直径所在直线都是圆的对称轴。

答案： 轴对称 直径

2. 垂径定理*：垂直于弦的直径平分弦,并且平分弦所对的两条弧。

答案： 直径 两条弧

3. 垂径定理的推论*：平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。

答案： 垂直于 平分 两条弧

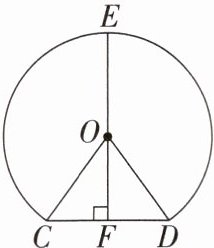
【例】“圆”是中国文化的一个重要精神元素,在中式建筑中,“圆”有着广泛的运用,最具代表性的便是园林中的门洞。如图24.1-3是某园林中的圆弧形门洞的数学模型,该圆弧形门洞的半径为1.3 m,E为圆上一点,$\overset{\frown}{CE}= \overset{\frown}{DE}$,$EF\perp CD$于点F,且$EF = 2.5$m,则门洞的跨径CD的长为(B)。

A.0.5 m
B.1 m
C.1.2 m
D.1.3 m

答案： 解析 由题意,得$OE = OC = OD = 1.3$m,又$EF = 2.5$m,所以$OF = 1.2$m。
因为$EF\perp CD$,所以$CF= \sqrt{OC^{2}-OF^{2}} = 0.5$m,所以$CD = 2CF = 1$m。故选B。
答案 B

* 跟踪练习 在直径为10 m的圆柱形油槽内注入一些油后,截面如图24.1-5所示,液面宽$AB = 6$m,如果继续向油槽内注油,使液面宽为8 m,那么液面上升的高度为(C)。

A.1 m
B.2 m
C.1 m或7 m
D.2 m或6 m

答案： C

1. 下列说法正确的是(B)。
A.直径是圆的对称轴
B.经过圆心的直线是圆的对称轴
C.与圆相交的直线是圆的对称轴
D.与半径垂直的直线是圆的对称轴

答案： B

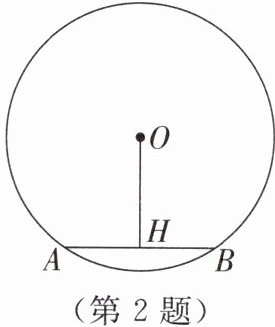
2. 如图,在半径为5的$\odot O$中,弦$AB = 6$,$OH\perp AB$于点H,则$OH= $(B)。

A.3
B.4
C.5
D.6

答案： B