《2025年伴你学山西九年级数学上册北师大版》

5. 如图所示的是胡老师画的一幅写生画,四位同学对这幅画的作画时间作了猜测.根据胡老师给出的方向坐标,猜测比较合理的是(C).


A.小明：“早上8点”
B.小亮：“中午12点”
C.小刚：“下午5点”
D.小红：“什么时间都行”

答案： C

6. 如图,灯光下有一个标语牌,小马在晚上用如下方法测量这个标语牌的高度：先量出标语牌在灯光下的影长,再找一根长度已知的竹竿,任意选定一个位置测量竹竿在这同一灯光下的影长,然后由标语牌的高度与其影长之比等于竹竿长与其影长之比即可求出标语牌的高度,他的方法错误.(填“正确”或“错误”)
]

答案： 错误

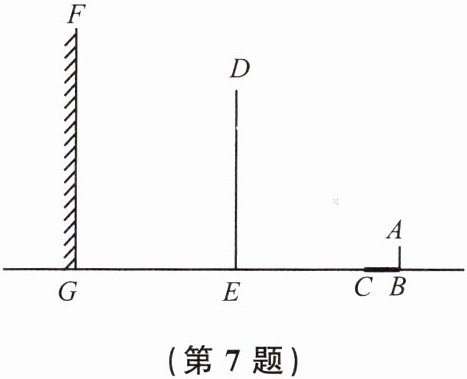
7. 如图,小亮的身高用线段AB表示,阳光下他在地面上的影子是线段BC,线段DE表示旗杆,线段FG表示一堵高墙.
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子；
(2)如果小亮的身高AB= 1.6m,他的影长BC= 2.4m,旗杆的高DE= 15m,旗杆与高墙的距离EG= 16m,求旗杆的影子落在墙上的长度.
]

答案：
解:
(1)如图,线段EG和MG为旗杆在同一时刻阳光照射下形成的影子.
　　　　　　　　　　　
(2)如图,过点G作GH//MD，交DE于点H，则四边形MDHG为平行四边形.
∴MG=DH.
∵太阳光为平行光线，
∴MD//AC，
∴HG//AC.
∴∠HGE=∠ACB.
　　又
∵∠DEG=∠ABC=90°，
∴△HGE∽△ACB，
∴$\frac{HE}{EG}=\frac{AB}{BC}$.
　　设旗杆的影子落在墙上的长度为$x$m.
∵AB = 1.6m，BC = 2.4m，DE = 15m，
　　EH = DE - DH = (15 - x)m，EG = 16m，
∴$\frac{15 - x}{16}=\frac{1.6}{2.4}$，解得$x=\frac{13}{3}$.
　　故旗杆的影子落在墙上的长度为$\frac{13}{3}$m.

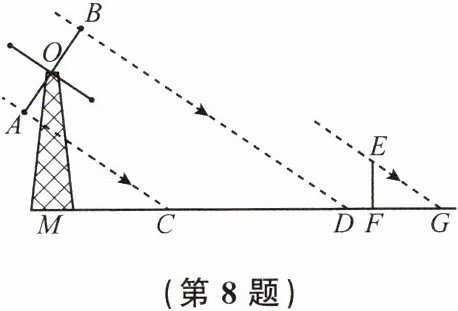
8. 如图所示的是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片OA,OB,此时各叶片在地面上形成的影子为线段CD,测得MC= 8.5m,CD= 13m,垂直于地面的木棒EF与影子FG的长度之比为2:3.
(1)求点O,M之间的距离；
(2)请求出转动时,叶片外端离地面的最大高度.
]

答案：
解:
(1)如图，过点O作OH//AC，交CD于点H，过点O作OJ//CD交BD于点J，过点B作BI⊥OJ，垂足为点I，延长MO到点K，使得OK = OB.
　　　　　
　　根据题意，点O是AB的中点.
∵OH//AC，AC//BD，
∴OH//AC//BD.
∴$\frac{AO}{OB}=\frac{CH}{HD}$，
∴点H是CD的中点.
∵CD = 13m，
∴CH = HD = $\frac{1}{2}$CD = 6.5m.
∴MH = MC + CH = 8.5 + 6.5 = 15m.
　　由题意知$\frac{EF}{FG}=\frac{OM}{MH}=\frac{2}{3}$.
∴$\frac{OM}{15}=\frac{2}{3}$，解得OM = 10m.
　　所以点O，M之间的距离等于10m.
(2)
∵BI⊥OJ，
∴∠BIO = ∠BIJ = 90°.
　　由题意知∠OBJ = ∠OBI + ∠JBI = 90°.
∵∠BOI + ∠OBI = 90°，
∴∠BOI = ∠JBI.
∴△BIO∽△JIB，
∴$\frac{BI}{IJ}=\frac{EF}{FG}=\frac{2}{3}$，
∴$\frac{BI}{IJ}=\frac{OI}{BI}=\frac{2}{3}$.
∴BI = $\frac{2}{3}$IJ，OI = $\frac{2}{3}$BI，
∴OI = $\frac{4}{9}$IJ.
∵OJ//CD，OH//DJ，
∴四边形OHDJ是平行四边形.
∴OJ = HD = 6.5m.
∵OJ = OI + IJ = $\frac{4}{9}$IJ + IJ = 6.5m，
∴IJ = 4.5m，BI = 3m，OI = 2m.
　　在Rt△OBI中，由勾股定理得$OB^2 = OI^2 + BI^2$.
∴OB = $\sqrt{OI^2 + BI^2}=\sqrt{2^2 + 3^2}=\sqrt{13}$（m）.
∴OB = OK = $\sqrt{13}$m.
　　所以MK = MO + OK = (10 + $\sqrt{13}$)m.
　　故叶片外端离地面的最大高度为(10 + $\sqrt{13}$)m.