《2025年伴你学山西九年级数学上册北师大版》

6. 如图 4-2-11,已知 $ l_1 // l_2 // l_3 $,$\frac{AB}{BC} = \frac{m}{n}$,求 $\frac{DE}{DF}$ 的值.

答案： 解：
∵$\frac{AB}{BC}=\frac{m}{n}$，
∴$\frac{AB}{AC}=\frac{m}{m+n}$. 又
∵$l_1// l_2// l_3$，
∴$\frac{DE}{DF}=\frac{AB}{AC}=\frac{m}{m+n}$.

7. 如图 4-2-12,线段 AB 的两个端点都是小正方形的顶点,按要求作图：
①仅用一把无刻度的直尺；②保留作图痕迹.
(1)在图甲中画出线段 AB 的二等分点 C；
(2)在图乙中画出线段 AB 的一个三等分点 D.

答案：
解：
(1)如图甲，点C即为所作.
(2)如图乙，点D即为所作.

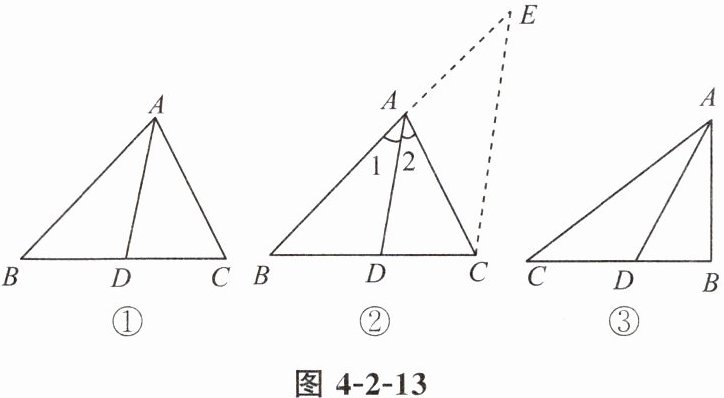
8. 如图 4-2-13 ①,在 △ABC 中,AD 平分 ∠BAC,则 $\frac{AB}{AC} = \frac{BD}{CD}$. 下面是部分证明过程.
证明：如图 4-2-13 ②,过点 C 作 CE//DA,交 BA 的延长线于点 E……
任务：
(1)请按照上面的证明思路,写出该证明的剩余部分；
(2)如图 4-2-13 ③,在 Rt△ABC 中,AB = 3,BC = 4,∠ABC = 90°,AD 平分 ∠BAC,则 △ABD 的周长等于$\frac{9+3\sqrt{5}}{2}$.

(1)证明：
∵CE//DA，
∴$\frac{BD}{CD}=\frac{BA}{EA}$，∠2=∠ACE，∠1=∠E.
∵∠1=∠2，
∴∠ACE=∠E，
∴AE=AC，
∴$\frac{AB}{AC}=\frac{BD}{CD}$.

答案：
(1)证明：
∵CE//DA，
∴$\frac{BD}{CD}=\frac{BA}{EA}$，∠2=∠ACE，∠1=∠E.
∵∠1=∠2，
∴∠ACE=∠E，
∴AE=AC，
∴$\frac{AB}{AC}=\frac{BD}{CD}$.
(2)$\frac{9+3\sqrt{5}}{2}$