第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 如图①,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为5m、宽为4m的矩形,将不规则图案围起来,然后在适当位置随机地朝矩形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或矩形区域外不计试验结果),他将若干次有效试验的结果绘制成了如图②所示的折线统计图,由此他估计不规则图案的面积为(
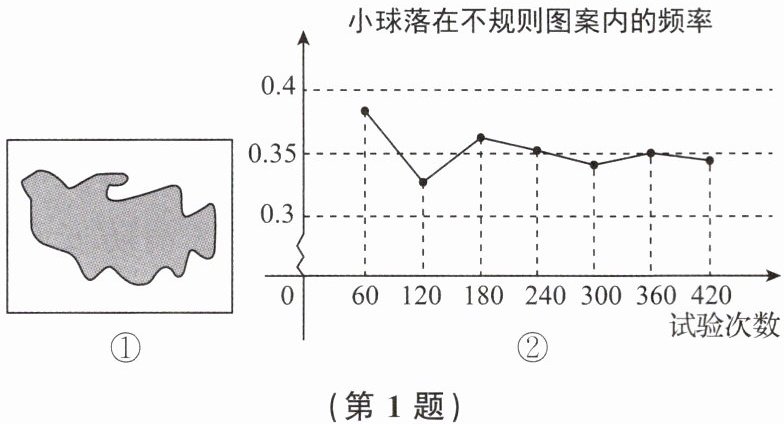
A.$6m^{2}$
B.$7m^{2}$
C.$8m^{2}$
D.$9m^{2}$
B
).
A.$6m^{2}$
B.$7m^{2}$
C.$8m^{2}$
D.$9m^{2}$
答案:
B
2. 从$-2$,$-1$,$2$这三个数中任取两个不同的数相乘,积为正数的概率是
$\frac{1}{3}$
.
答案:
$\frac{1}{3}$
1. 某市体育中考男生抽测项目规则:从立定跳远、掷实心球、引体向上中随机抽取一项;从$50m$,$50m×2$,$100m$中随机抽取一项. 恰好抽中掷实心球和$50m$的概率是(
A.$\frac{1}{3}$
B.$\frac{1}{6}$
C.$\frac{2}{3}$
D.$\frac{1}{9}$
D
).A.$\frac{1}{3}$
B.$\frac{1}{6}$
C.$\frac{2}{3}$
D.$\frac{1}{9}$
答案:
D
2. 端午节是我国的传统佳节,民间历来有吃粽子的习俗. 现有外形完全相同的肉馅粽、豆沙馅粽、红枣馅粽和蛋黄馅粽各一个. 煮熟后,小王随意吃了其中的两个,小王第二个吃到的恰好是红枣馅粽的概率为
$\frac{1}{4}$
.
答案:
$\frac{1}{4}$
3. 某批羽毛球的质量检查结果如下表:
|抽取的羽毛球数$a$|100|200|400|600|800|1000|1200|
|优等品的频数$b$|93|192|380|561|752|941|1128|
|优等品的频率$\frac{b}{a}$|0.930|0.960|0.950|0.935|0.940|0.941|0.940|
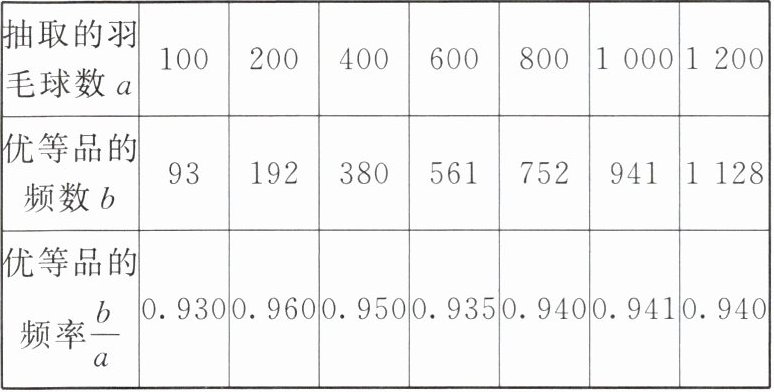
小明估计,从这批羽毛球中任意抽取的一个羽毛球是优等品的概率是0.94. 下列说法正确的是(
A.如果继续对这批羽毛球进行质量检查,优等品的频率将在0.94附近摆动
B.从这批羽毛球中任意抽取一个,一定是优等品
C.从这批羽毛球中任意抽取50个,优等品有47个
D.从这批羽毛球中任意抽取1100个,优等品的频率在$0.940~0.941$的范围内
|抽取的羽毛球数$a$|100|200|400|600|800|1000|1200|
|优等品的频数$b$|93|192|380|561|752|941|1128|
|优等品的频率$\frac{b}{a}$|0.930|0.960|0.950|0.935|0.940|0.941|0.940|

小明估计,从这批羽毛球中任意抽取的一个羽毛球是优等品的概率是0.94. 下列说法正确的是(
A
).A.如果继续对这批羽毛球进行质量检查,优等品的频率将在0.94附近摆动
B.从这批羽毛球中任意抽取一个,一定是优等品
C.从这批羽毛球中任意抽取50个,优等品有47个
D.从这批羽毛球中任意抽取1100个,优等品的频率在$0.940~0.941$的范围内
答案:
A
4. 一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数. 投掷两次,向上一面的点数依次记为$a$,$b$,那么方程$x^{2}+ax + b = 0$有解的概率是(
A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{8}{15}$
D.$\frac{19}{36}$
D
).A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{8}{15}$
D.$\frac{19}{36}$
答案:
D
查看更多完整答案,请扫码查看


