《2025年伴你学山西九年级数学上册北师大版》

10. 阅读下面材料,解决相关问题.
下图是一个三角点阵,从上往下数有无数行,其中第一行有$1$个点,第二行有$2$个点……第$n行有n$个点.

容易发现,三角点阵中前$4行的点数之和为10$.
(1)探索：三角点阵中前$8$行的点数之和为36,前$15$行的点数之和为120,前$n$行的点数之和为$\dfrac{1}{2}n(n+1)$；
(2)体验：三角点阵中前$n$行的点数之和不能(填“能”或“不能”)为$500$；
(3)运用：某广场要摆放若干种造型的盆景,其中一种造型要用$420$盆同样规格的花,若按照第一排$2$盆,第二排$4$盆,第三排$6$盆……第$n排2n$盆的规律摆放,一共能摆放20排.

答案：
(1)36 120 $\dfrac{1}{2}n(n+1)$
(2)不能
(3)20排

11. 如图①,要设计一幅长$30\mathrm{cm}$、宽$20\mathrm{cm}$的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为$2:3$. 如果要使所有彩条所占面积为原矩形图案面积的$\frac{1}{3}$,应如何设计每个彩条的宽度？

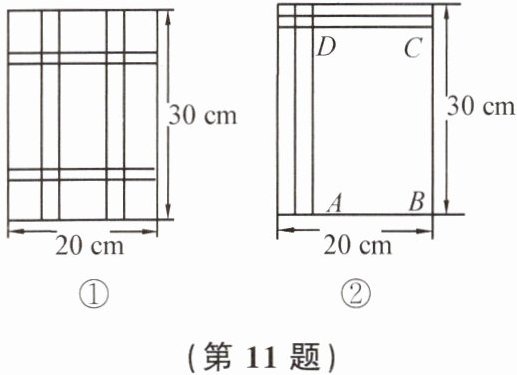
分析：由横、竖彩条的宽度比为$2:3$,可设每个横彩条的宽为$2x\mathrm{cm}$,则每个竖彩条的宽为$3x\mathrm{cm}$. 为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图②所示的情况,得到矩形$ABCD$.
结合以上分析完成填空：如图②,用含$x$的代数式表示：
$AB = $$(20-6x)cm$；$AD = $$(30-4x)cm$；
矩形$ABCD的面积= $$(24x^{2}-260x+600)cm^{2}$.
列出方程并完成本题的解答.
根据题意，得$24x^{2}-260x+600=\left(1-\dfrac{1}{3}\right)×20×30$.整理，得$6x^{2}-65x+50=0$.解方程，得$x_{1}=\dfrac{5}{6}$，$x_{2}=10$(舍去).此时$2x=\dfrac{5}{3}$，$3x=\dfrac{5}{2}$.故每个横、竖彩条的宽度分别为$\dfrac{5}{3}cm$，$\dfrac{5}{2}cm$.

答案： $(20-6x)cm$ $(30-4x)cm$ $(24x^{2}-260x+600)cm^{2}$ 根据题意，得$24x^{2}-260x+600=\left(1-\dfrac{1}{3}\right)×20×30$.整理，得$6x^{2}-65x+50=0$.解方程，得$x_{1}=\dfrac{5}{6}$，$x_{2}=10$(舍去).此时$2x=\dfrac{5}{3}$，$3x=\dfrac{5}{2}$.故每个横、竖彩条的宽度分别为$\dfrac{5}{3}cm$，$\dfrac{5}{2}cm$.