《2025年伴你学山西九年级数学上册北师大版》

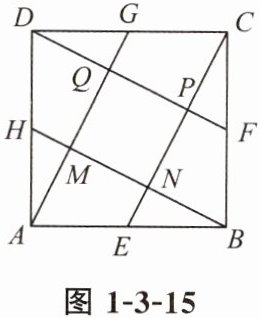
5. 如图1-3-15,边长为5的正方形ABCD,E,F,G,H分别为各边中点,连接AG,BH,CE,DF,交点分别为点M,N,P,Q,四边形MNPQ的面积为(C)。

A.1
B.2
C.5
D.10

答案： C

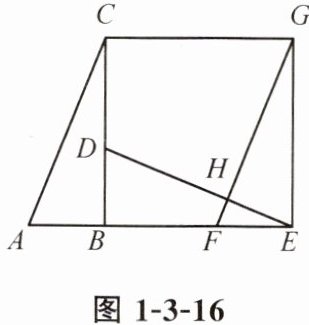
6. 如图1-3-16,在Rt△ABC中,∠ABC= 90°,先把△ABC绕点B顺时针旋转90°后至△DBE,再把△ABC沿射线AB平移至△FEG,且DE与FG相交于点H。
(1)判断DE与FG的位置关系,并说明理由；
(2)连接CG,证明四边形CBEG是正方形。

答案：
(1)解:DE⊥FG.理由如下:由题意,得∠ABC=∠DBE=90°,∠A=∠BDE=∠GFE,
∴∠BDE+∠BED=90°.
∴∠GFE+∠BED=90°.
∴∠FHE=90°,即DE⊥FG.
(2)证明:
∵△ABC沿射线AB平移至△FEG,
∴CB//GE,CB=GE.
∴四边形CBEG是平行四边形.又
∵∠ABC=∠GEF=90°,
∴□CBEG是矩形又
∵BC=BE,
∴四边形CBEG是正方形.

7. 问题情境：
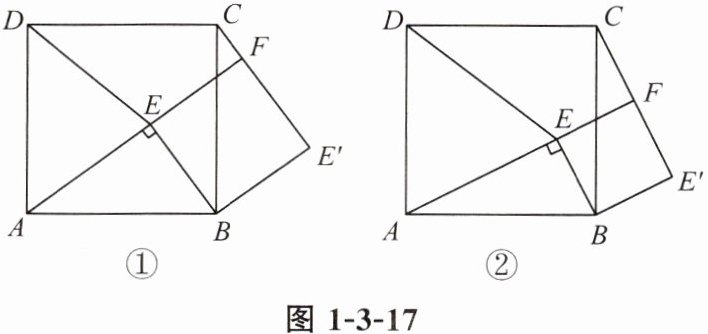
如图1-3-17①,点E为正方形ABCD内一点,∠AEB= 90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBE'(点A的对应点为点C)。延长AE交CE'于点F,连接DE。
猜想证明：
(1)试判断四边形BE'FE的形状,并说明理由；
(2)如图1-3-17②,若DA= DE,请猜想线段CF与E'F的数量关系并加以证明。

答案：
(1)四边形BE'FE是正方形.理由如下:
∵将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBE'(点A的对应点为点C),
∴∠AEB=∠CE'B=90°,BE=BE',∠EBE'=90°.又
∵∠BEF=90°,
∴四边形BE'FE是矩形
∵BE=BE',
∴四边形BE'FE是正方形
(2)CF=E'F.证明如下:如图,过点D作DH⊥AE于点H.
∵DA=DE,DH⊥AE,
∴AH= $\frac{1}{2}$AE,
∴∠ADH+∠DAH=90°.
∵四边形ABCD是正方形，
∴AD=AB,∠DAB=90°.
∴∠DAH+∠EAB=90°,
∴∠ADH=∠EAB.又
∵∠AHD=∠AEB=90°,
∴△ADH≌△BAE(AAS),
∴AH=BE= $\frac{1}{2}$AE.
∵将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBE'(点A的对应点为点C),
∴AE=CE'.由
(1)知四边形BE'FE是正方形，
∴BE=E'F.
∴E'F= $\frac{1}{2}$CE',
∴CF=E'F.