第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 点 $ C $ 把线段 $ AB $ 分成两条线段 $ AC $ 和 $ BC $,如果 $ \frac{AC}{AB} = \frac{BC}{AC} $,那么称线段 $ AB $ 被点 $ C $ 黄金分割,$ AC $ 与 $ AB $ 的比叫做黄金比,其比值是(
A.$ \frac{\sqrt{5} - 1}{2} $
B.$ \frac{3 - \sqrt{5}}{2} $
C.$ \frac{\sqrt{5} + 1}{2} $
D.$ \frac{3 + \sqrt{5}}{2} $
A
).A.$ \frac{\sqrt{5} - 1}{2} $
B.$ \frac{3 - \sqrt{5}}{2} $
C.$ \frac{\sqrt{5} + 1}{2} $
D.$ \frac{3 + \sqrt{5}}{2} $
答案:
A
2. 已知点 $ C $ 是线段 $ AB $ 的黄金分割点,$ AC > BC $,$ AB = 2 $,则 $ AC $ 的长为
$\sqrt{5}-1$
.
答案:
$\sqrt{5}-1$
3. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”. 如图 4 - 4 - 25,$ P $ 为 $ AB $ 的黄金分割点$(AP > PB)$,如果 $ AB $ 的长度为 $ 8 cm $,那么 $ AP $ 的长为
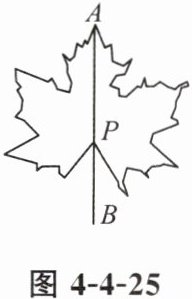
$(4\sqrt{5}-4)cm$
.
答案:
$(4\sqrt{5}-4)cm$
1. 若点 $ C $ 是 $ AB $ 的黄金分割点,且 $ AC > BC $,则下列等式成立的是(
A.$ AB^{2} = AC \cdot BC $
B.$ BC^{2} = AC \cdot AB $
C.$ AC^{2} = BC \cdot AB $
D.$ BC = \frac{\sqrt{5} - 1}{2}AB $
C
).A.$ AB^{2} = AC \cdot BC $
B.$ BC^{2} = AC \cdot AB $
C.$ AC^{2} = BC \cdot AB $
D.$ BC = \frac{\sqrt{5} - 1}{2}AB $
答案:
C
2. 在图 4 - 4 - 26①中,$ AB = 2 $,点 $ C $ 在线段 $ AB $ 上,且满足 $ \frac{AC}{AB} = \frac{BC}{AC} $. 如图 4 - 4 - 26②,以图 4 - 4 - 26①中的 $ AC $,$ BC $ 为邻边构建矩形 $ ACBF $,以 $ CB $ 长为边构建正方形 $ CBDE $,则矩形 $ AEDF $ 的面积为(
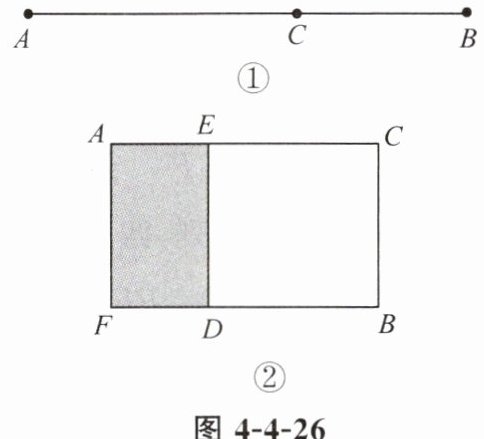
A.$ 14 - 6\sqrt{5} $
B.$ 4\sqrt{5} - 8 $
C.$ 10\sqrt{5} - 22 $
D.$ 10\sqrt{5} - 20 $
C
).
A.$ 14 - 6\sqrt{5} $
B.$ 4\sqrt{5} - 8 $
C.$ 10\sqrt{5} - 22 $
D.$ 10\sqrt{5} - 20 $
答案:
C
3. 如图 4 - 4 - 27,某品牌汽车为了打造更加精美的外观,特将汽车倒车镜设计在整个车身黄金分割点的位置,若车头与倒车镜的水平距离为 $ 1.58 m $,则该车车身总长约为
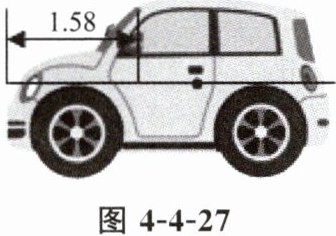
4.14 m
.(结果精确到 $ 0.01 m $)
答案:
4.14 m
4. 某公司生产了一种新型手杖,长为 $ 1.2 m $,现要在其黄金分割点的位置安放一个小装饰品,则手柄与小饰品的距离约为
0.46 m
.(装饰品离手杖的上端较近,结果精确到 $ 0.01 m $)
答案:
0.46 m
5. 鹦鹉螺曲线的每个半径和后一个半径的比都是黄金比例. 如图 4 - 4 - 28,$ P $ 是 $ AB $ 的黄金分割点$(AP > BP)$,若线段 $ AB $ 的长为 $ 4 cm $,则 $ AP $ 的长为(
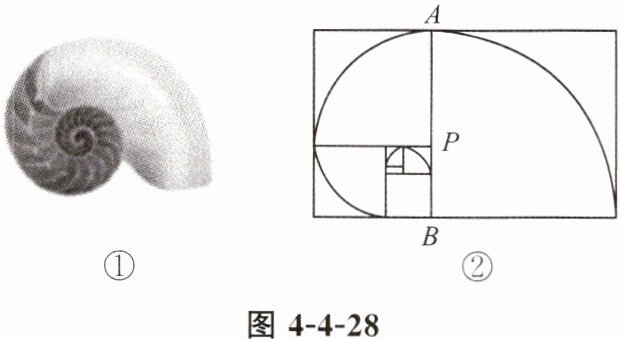
A.$ 2\sqrt{5} - 2 $
B.$ 2\sqrt{5} + 1 $
C.$ 6 - 2\sqrt{5} $
D.$ 2\sqrt{5} - 1 $
A
).
A.$ 2\sqrt{5} - 2 $
B.$ 2\sqrt{5} + 1 $
C.$ 6 - 2\sqrt{5} $
D.$ 2\sqrt{5} - 1 $
答案:
A
查看更多完整答案,请扫码查看


