《2025年伴你学山西九年级数学上册北师大版》

4. 在同一时刻,把两根长度不等的杆子置于阳光下,如果它们的影长相等,那么这两根杆子的相对位置是(C)。
A.两根都垂直于地面
B.两根平行斜插在地上
C.两根杆子不平行
D.一根倒在地上

答案： C

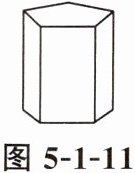
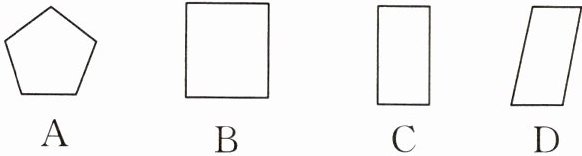
5. 一个正五棱柱如图 5 - 1 - 11 所示,当投射线由正前方射到后方时,它的正投影是(B)。

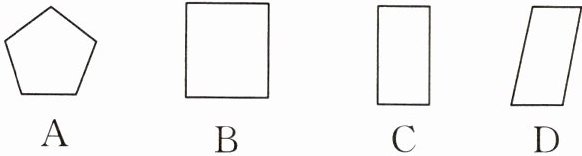
答案： B

6. 早上练习跑步时,如果你的影子总是在你的正前方,那么你跑步的方向是西。

答案： 西

7. 小明和爸爸在公园散步,此时爸爸的影子落在了身后的地面和墙上,如图 5 - 1 - 12①。其中,$ BC $ 段为地上的影子,$ AC $ 段为墙上的影子。小明想利用所学知识测量出爸爸的身高。他向工作人员询问得知：公园地面与墙面所用的砖块均厚 $ 13.5 $ cm,长 $ 65 $ cm。经过测量,小明发现 $ BC $ 段刚好是 $ 4 $ 块地砖的长度,$ AC $ 段恰好为 $ 4 $ 块地砖的厚度。同一时刻,小明观察到公园门口指示牌影子的顶端刚好到达保安亭,如图 5 - 1 - 12②,其中 $ MN $ 为指示牌的影子。已知爸爸、墙面、指示牌和保安亭均与地面垂直,指示牌高 $ 2 $ m,指示牌距保安亭 $ 4 $ m,请你根据以上信息,帮小明求出爸爸的身高。

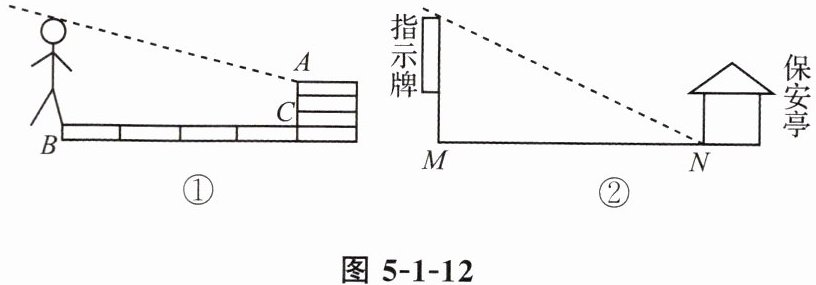
答案：
解:如图,过点A作AE⊥BD,垂足为点E.
∵四边形ACBE为矩形,
∴AC=BE=4×13.5=54(cm),AE=BC=4×65=260(cm).
∵指示牌高2m,指示牌距保安亭4m,
∴$\frac{DE}{AE}=\frac{2}{4}=\frac{1}{2}$.
　　　　　　　　　　　　　　
∴DE=$\frac{1}{2}$AE=130cm.
∴BD=DE+BE=130+54=184(cm).
　故爸爸的身高为184cm.

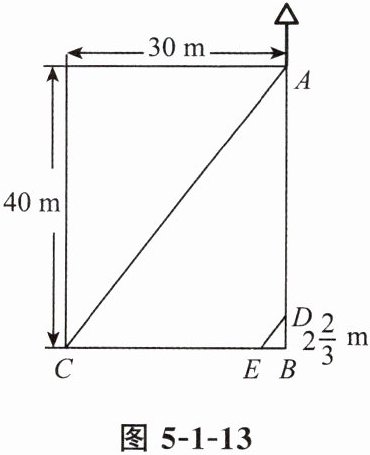
8. 如图 5 - 1 - 13,在一个长 $ 40 $ m、宽 $ 30 $ m 的矩形小操场上,王刚从 $ A $ 地出发,沿着 $ A \to B \to C $ 的路线以 $ 3 $ m/s 的速度跑向 $ C $ 地。当他出发 $ 4 $ s 后,张华有东西需要交给他,就从 $ A $ 地出发沿王刚走的路线追赶。当张华跑到距 $ B $ 地 $ 2 \frac{2}{3} $ m 的 $ D $ 处时,他和王刚在阳光下的影子恰好重叠在同一条直线上。此时,$ A $ 处一根电线杆在阳光下的影子也恰好落在对角线 $ AC $ 上。
(1)求他们的影子重叠时,两人相距多少米($ DE $ 的长)；
(2)求张华追赶王刚的速度是多少(结果精确到 $ 0.1 $ m/s)。

答案： 解:
(1)根据题意，DE//AC,
∴∠BED=∠BCA.
　又
∵∠B=∠B,
∴△DEB∽△ACB,
∴$\frac{DE}{AC}=\frac{BD}{BA}$.
　在Rt△ABC中,AB=40m,BC=30m,BD=$2\frac{2}{3}$m.
∴AC=50m,
∴$\frac{DE}{50}=\frac{2\frac{2}{3}}{40}$,解得DE=$\frac{10}{3}$m.
　故他们的影子重叠时，两人相距$\frac{10}{3}$m.
(2)根据题意,得DE²=BD²+BE².
∵DE=$\frac{10}{3}$m,BD=$2\frac{2}{3}$m,
∴BE=2m,
∴s_{王}=AB+BE=42m.
∴t_{王}=14s,
∴t_{张}=10s.
∵s_{张}=AD=AB−BD=$\frac{112}{3}$m,
∴v_{张}≈3.7m/s.
　故张华追赶王刚的速度约是3.7m/s.