《2025年伴你学山西九年级数学上册北师大版》

3. 如图 2 - 3 - 2,有一块矩形硬纸板,长 $30$ cm,宽 $20$ cm. 在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子. 当剪去的正方形的边长取何值时,所得长方体盒子的侧面积为 $200$ cm^2?

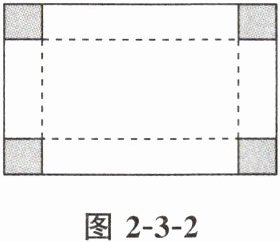
答案： 解：设剪去的正方形的边长为x cm，则制成无盖长方体盒子的底面长为(30-2x)cm，宽为(20-2x)cm，高为x cm.依题意，得2×[(30-2x)+(20-2x)]x=200.整理，得2x²-25x+50=0.解得x₁=5/2，x₂=10.当x=10时，20-2x=0，不合题意，舍去.故x=5/2.故当剪去的正方形的边长为5/2cm时，所得长方体盒子的侧面积为200cm².

4. 在美化校园的活动中,某兴趣小组想借助如图 2 - 3 - 3 所示的直角墙角(两边足够长),用 $28$ m 长的篱笆围成一个矩形花园 $ABCD$ (篱笆只围 $AB$,$BC$ 两边),设 $AB = x$ m. 若花园的面积为 $192$ m^2,求 $x$ 的值.

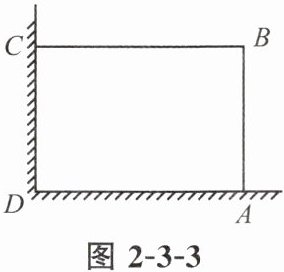
答案： 解：由题意，得x(28-x)=192.解得x₁=12，x₂=16.

5. 如图 2 - 3 - 4,用同样规格的黑白两色的正方形瓷砖铺设矩形地面. 请观察下列图形并解答有关问题：
(1)在第 $n$ 个图中,每一横行共有 n+3块瓷砖,每一竖列共有 n+2块瓷砖(均用含 $n$ 的代数式表示).
(2)设铺设地面所用瓷砖的总块数为 $y$,请写出 $y$ 与(1)中的 $n$ 的函数关系式(不要求写自变量 $n$ 的取值范围).
$y=(n+3)(n+2)$，即$y=n²+5n+6$
(3)按上述铺设方案,铺一块这样的矩形地面共用了 $506$ 块瓷砖,求此时 $n$ 的值.
当$y=506$时，$n²+5n+6=506$，解得$n₁=20$，$n₂=-25$(舍去)
(4)若黑瓷砖每块 $4$ 元,白瓷砖每块 $3$ 元,在问题(3)中,共需花多少元购买瓷砖?
白瓷砖块数是420，黑瓷砖块数是86，共需1604元
(5)判断是否存在黑瓷砖与白瓷砖块数相等的情形,并说明理由.
不存在.理由如下：$n(n+1)=(n+3)(n+2)-n(n+1)$，化简为$n²-3n-6=0$，解得$n₁=(3+\sqrt{33})/2$，$n₂=(3-\sqrt{33})/2$(舍去).
∵$n$的值不为正整数，
∴不存在黑瓷砖与白瓷砖块数相等的情形

答案：
(1)(n+3)(n+2)
(2)y=(n+3)(n+2)，即y=n²+5n+6.
(3)当y=506时，n²+5n+6=506，解得n₁=20，n₂=-25(舍去).
(4)白瓷砖块数是420，黑瓷砖块数是86，共需1604元.
(5)不存在.理由如下：n(n+1)=(n+3)(n+2)-n(n+1)，化简为n²-3n-6=0，解得n₁=(3+√33)/2，n₂=(3-√33)/2(舍去).
∵n的值不为正整数，
∴不存在黑瓷砖与白瓷砖块数相等的情形.

6. 计划在一块长 $16$ m、宽 $12$ m 的矩形荒地上建造一个花园,要求花园面积是荒地面积的一半,如图 2 - 3 - 5 分别是小华与小芳的设计方案. 在小组讨论时,同学们都认为小华的方案是正确的,但对小芳的方案是否符合条件有不同意见,你认为小芳的方案符合条件吗? 若不符合,请你依照小芳的方案设计小路的宽度.

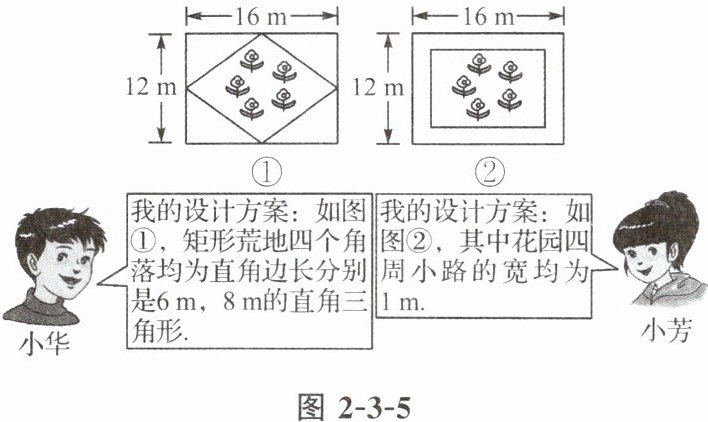
答案： 解：不符合.设小路的宽度均为x m，则花园的长为(16-2x)m，宽为(12-2x)m.根据题意，得(16-2x)(12-2x)=1/2×16×12.解得x₁=2，x₂=12(舍去).故小芳的方案不符合条件，小路的宽度应为2m.