《2025年名校作业九年级数学上册人教版湖北专版》

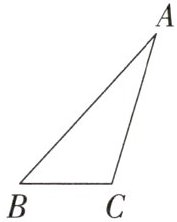
1.如图,在△ABC中,∠ABC= 45°,AB= 7,BC= 3.
(1)画出将线段AC绕点A沿逆时针旋转90°后的线段AD,将线段AB绕点A沿顺时针旋转90°后的线段AE,连接CD,BE,BD,CE.
(2)求BD的长.

答案：

（1）作图如下：

（此处需根据题目要求进行作图，由于无法直接绘制图形，故文字描述作图步骤：以点A为旋转中心，将线段AC绕点A逆时针旋转90°得到线段AD；将线段AB绕点A顺时针旋转90°得到线段AE，然后依次连接CD、BE、BD、CE）

（2）过点A作AF⊥BC交BC的延长线于点F，设CF = x。

因为∠ABC = 45°，∠AFB = 90°，所以△ABF是等腰直角三角形，AF = BF = BC + CF = 3 + x。

在Rt△AFC中，根据勾股定理得：AF² + CF² = AC²，即(3 + x)² + x² = AC² ①。

在Rt△ABF中，AB² = AF² + BF²，AB = 7，所以7² = (3 + x)² + (3 + x)²，即49 = 2(3 + x)²，解得(3 + x)² = 49/2，3 + x = 7√2/2（负值舍去），所以AF = BF = 7√2/2，x = 7√2/2 - 3。

将x = 7√2/2 - 3代入①得：AC² = (7√2/2)² + (7√2/2 - 3)²。

因为AD是AC绕点A逆时针旋转90°得到的，所以AD = AC，∠CAD = 90°。

AE是AB绕点A顺时针旋转90°得到的，所以AE = AB = 7，∠BAE = 90°，所以∠DAE = 360° - ∠CAD - ∠BAE - ∠BAC = 360° - 90° - 90° - ∠BAC = 180° - ∠BAC。

在△ABD中，根据余弦定理得：BD² = AB² + AD² - 2AB·AD·cos∠BAD。

因为∠BAD = ∠BAC + ∠CAD = ∠BAC + 90°，所以cos∠BAD = cos(∠BAC + 90°) = -sin∠BAC。

在Rt△AFC中，sin∠BAC = CF / AC = x / AC，所以BD² = AB² + AC² + 2AB·AC·(x / AC) = AB² + AC² + 2AB·x。

将AB = 7，AC² = (7√2/2)² + (7√2/2 - 3)²，x = 7√2/2 - 3代入得：

BD² = 7² + [(7√2/2)² + (7√2/2 - 3)²] + 2×7×(7√2/2 - 3)，经过计算化简得BD² = 58，所以BD = √58。

√58

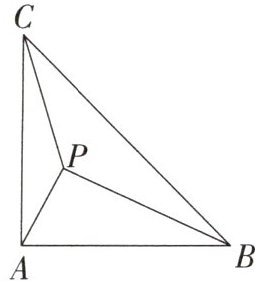
2.如图,在等腰三角形ABC中,∠CAB= 90°,点P是△ABC内一点,AP= 1,BP= 3,CP= √7.
(1)画出将△APB绕点A逆时针旋转90°后的△AQC;
(2)求∠APC的度数.

答案： ∠APC=135°。

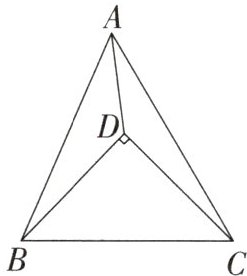
3.如图,点D是△ABC内一点,∠BDC= 90°,BD= CD,AB= 20,AC= 21,AD= 13√2/2,求BC的长.

答案： 解：
将△ADC绕点D顺时针旋转90°，使点C与点B重合，得△EDB，连接AE。
∵旋转性质，
∴DE=DA，∠ADE=90°，EB=AC=21，△ADE为等腰直角三角形。
∵AD=13√2/2，
∴AE=√(AD²+DE²)=√[2×(13√2/2)²]=13。
在△ABE中，AB=20，BE=21，AE=13，由余弦定理：
cos∠AEB=(AE²+BE²-AB²)/(2·AE·BE)=(13²+21²-20²)/(2×13×21)=5/13，
则sin∠AEB=12/13。
在△DEB中，DE=AD=13√2/2，∠DEB=45°-∠AEB，
cos∠DEB=cos(45°-∠AEB)=√2/2(cos∠AEB+sin∠AEB)=17√2/26。
由余弦定理EB²=DE²+DB²-2·DE·DB·cos∠DEB，设BD=x：
21²=(13√2/2)²+x²-2×(13√2/2)·x·(17√2/26)，
化简得x²-17x-631/2=0，解得x=29√2/2（负值舍去）。
∵△BDC为等腰直角三角形，
∴BC=√2·BD=29。
BC=29