《2025年名校作业九年级数学上册人教版湖北专版》

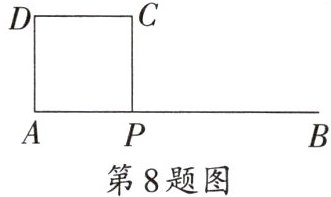
8.如图,线段AB= 10 cm,点P在线段AB上(不与点A,B重合),以AP为边作正方形APCD.设AP= x cm,BP= y cm,正方形APCD的面积为$ S cm^2 $,则y与x,S与x之间满足的函数关系分别是 (B)

A.一次函数关系、一次函数关系
B.一次函数关系、二次函数关系
C.二次函数关系、二次函数关系
D.二次函数关系、一次函数关系

答案： B

9.如图,某农场要盖三间长方形羊圈,打算一面利用旧墙(旧墙足够长),其余各面用木材围成栅栏.已知该农场现有木材可围成总长为24 m的栅栏.设三间羊圈的总面积为$ S(m^2) $,垂直于墙的一边长为$ x(m) $,则S关于x的函数关系式为$S=-4x^{2}+24x(0 ＜ x ＜ 6)$(写出自变量的取值范围).

答案： $S=-4x^{2}+24x(0 ＜ x ＜ 6)$

10.某学校准备将一块长20 m,宽14 m的矩形绿地扩建.设长和宽都增加x m,面积增加$ y m^2 $.
(1)求y与x之间的关系式.
(2)若要使绿地面积增加72 $ m^2 $,则长与宽都要增加多少？

答案：
(1)原矩形绿地的面积为 $20 × 14 = 280 m^2$。
扩建后的矩形绿地的长为 $(20+x)m$，宽为 $(14+x)m$。
扩建后的矩形绿地的面积为 $(20+x)(14+x) m^2$。
面积增加 $y m^2$，则：
$y = (20+x)(14+x) - 280$，
$y = 280 + 20x + 14x + x^2 - 280$，
$y = x^2 + 34x$。
所以，$y$ 与 $x$ 之间的关系式为 $y = x^2 + 34x$。
(2)要使绿地面积增加 $72 m^2$，
即 $y = 72$，代入 $y = x^2 + 34x$ 得：
$x^2 + 34x = 72$，
$x^2 + 34x - 72 = 0$，
通过求解这个一元二次方程，得到：
$x_{1} = 2, x_{2} = -36$，
由于 $x$ 表示增加的长度，不能为负，所以 $x = -36$ 不符合题意，舍去。
因此，长与宽都要增加 $2m$。

11.如图,某校要在一片空地处建梯形苗圃ABCD,其中两边AB,AD借用夹角为135°的两面墙(墙足够长),另外两边是总长为30 m的铁栅栏,已知AD//BC,∠C= 90°.
(1)求梯形苗圃ABCD的面积$ y(m^2) 与高 x(m) $之间的关系式；
(2)求x的取值范围.

答案：
(1)设梯形的高$CD = x$，铁栅栏总长为$BC + CD = 30$，则$BC = 30 - x$。过点$A$作$AE \perp BC$于点$E$，则$AE = CD = x$，四边形$AECD$为矩形，$AD = EC$。因为$\angle BAD = 135^\circ$，所以$\angle BAE = 135^\circ - 90^\circ = 45^\circ$，$\triangle ABE$为等腰直角三角形，$BE = AE = x$，故$AD = BC - BE = (30 - x) - x = 30 - 2x$。梯形面积$y = \frac{(AD + BC) \cdot CD}{2} = \frac{(30 - 2x + 30 - x)x}{2} = \frac{(60 - 3x)x}{2} = -\frac{3}{2}x^2 + 30x$。
(2)由$AD = 30 - 2x ＞ 0$得$x ＜ 15$，且$x ＞ 0$，故$x$的取值范围是$0 ＜ x ＜ 15$。
(1)$y = -\frac{3}{2}x^2 + 30x$；
(2)$0 ＜ x ＜ 15$。