《2025年名校作业九年级数学上册人教版湖北专版》

7. 某超市今年1月份的收入为50万元,第一季度总收入为175万元,问2,3月份平均每月的增长率为多少. 设平均每月的增长率为x,根据题意可列方程为$50 + 50(1+x) + 50(1+x)^2 = 175$.

答案： $50 + 50(1+x) + 50(1+x)^2 = 175$

8. 我国快递行业迅速发展,经调查,某快递公司今年5月份投递快递总件数为20万件,7月份投递快递总件数为33.8万件,假设该公司每月投递快递总件数的增长率相同.
(1)求该公司投递快递总件数的月增长率；
(2)如果该公司每月投递快递总件数的增长率保持不变,那么8月份投递快递总件数能否达到45万件？请说明理由.

答案：
(1) 设该公司投递快递总件数的月增长率为 $x$。
根据题意，5月份到7月份经过两个月，所以增长后的快递总件数可以表示为：
$20(1 + x)^{2} = 33.8$
展开方程得：
$(1 + x)^{2} = 1.69$
进一步求解，得到两个解：
$x_{1} = 0.3, \quad x_{2} = -2.3$
由于增长率不能为负，所以 $x_{2} = -2.3$ 不符合题意，舍去。
因此，该公司投递快递总件数的月增长率为 $30\%$。
(2) 根据第一问求得的月增长率 $x = 0.3$，我们可以计算8月份的快递总件数。
7月份的快递总件数为33.8万件，所以8月份的快递总件数可以表示为：
$33.8 × (1 + 0.3) = 43.94 (万件)$
由于 $43.94 ＜ 45$，
所以8月份的快递总件数不能达到45万件。

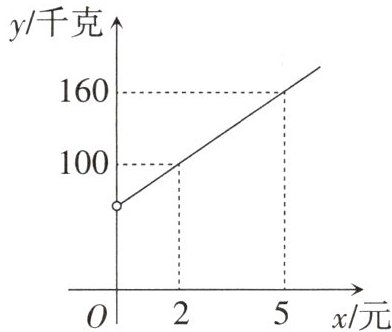
9. 某超市以每千克40元的价格购进一批榴莲,计划以每千克60元的价格销售,为了让顾客得到实惠,现决定降价销售. 已知这种榴莲的销售量y(千克)与每千克降价x(元)(0＜x＜20)之间满足如图所示的一次函数关系.

(1)求y与x之间的函数关系式.
(2)当每千克榴莲降价4元时,超市获利多少元？
(3)若超市要想获利2400元,且让顾客获得最大实惠,这种榴莲每千克应降价多少元？

答案：
(1)设y与x的函数关系式为y=kx+b，由图可知函数图像过点(2,100)和(5,160)，代入得：
$\begin{cases}2k + b = 100 \\5k + b = 160\end{cases}$
解得$k=20$，$b=60$，$\therefore y=20x+60$。
(2)当$x=4$时，$y=20×4 + 60=140$，每千克利润为$60 - 4 - 40=16$元，获利$16×140=2240$元。
(3)由题意得$(20 - x)(20x + 60)=2400$，整理得$x^2 - 17x + 60=0$，解得$x_1=5$，$x_2=12$，$\because$让顾客获得最大实惠，$\therefore x=12$。

10. 为丰富学生的学习生活,某校九年级组织学生参加黄鹤楼一日游活动,所联系的旅行社收费标准如下：

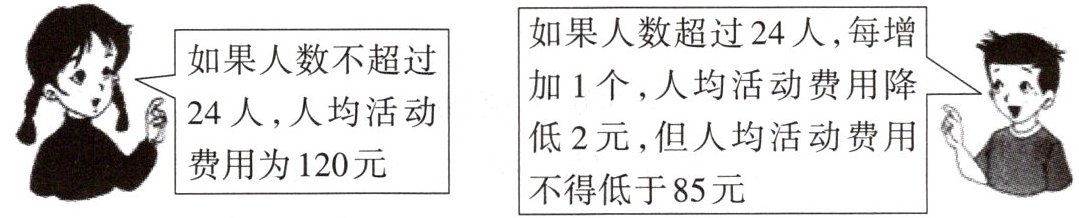
活动结束后,该班共支付该旅行社活动费用3520元,则该班参加这次旅行活动的共有多少人？

答案： 40