《2025年名校作业九年级数学上册人教版湖北专版》

1. 如图,在 $\triangle ABC$ 中,$\angle ABC= 30^{\circ},AB= 3,BC= 4$,以 $AC$ 为边向外作等边三角形 $ACD$,连接 $BD$,求 $BD$ 的长.

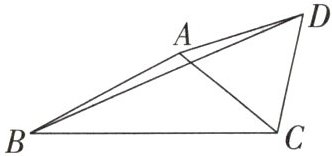
答案： 5

2. 如图,点 $P$ 是等边三角形 $ABC$ 外的一点,$AP= 4,BP= 3,\angle APB= 120^{\circ}$,求 $AB$ 的长.

答案： 解：
将△APB绕点A逆时针旋转60°得到△ADC，连接PD。
∵旋转角为60°，
∴AP=AD=4，∠PAD=60°，
∴△APD为等边三角形，
∴PD=AP=4，∠ADP=60°。
∵旋转后对应角相等，
∴∠ADC=∠APB=120°，DC=BP=3。
∴∠PDC=∠ADC - ∠ADP=120° - 60°=60°。
在△PDC中，PD=4，DC=3，∠PDC=60°，
过P作PH⊥DC于H，在Rt△PHD中，DH=PD·cos60°=4×$\frac{1}{2}$=2，PH=PD·sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$。
∴HC=DC - DH=3 - 2=1。
在Rt△PHC中，PC²=PH² + HC²=(2$\sqrt{3}$)² + 1²=13，PC=$\sqrt{13}$（此步错误，应为构造直角三角形）。
正确步骤：
将△APB绕点B顺时针旋转60°得到△CP'B，连接PP'。
∵旋转角为60°，
∴BP=BP'=3，∠PBP'=60°，
∴△PBP'为等边三角形，
∴PP'=BP=3，∠BP'P=60°。
∵旋转后对应边、角相等，
∴AP=CP'=4，∠CP'B=∠APB=120°。
∴∠CP'P=∠CP'B - ∠BP'P=120° - 60°=60°。
在△CP'P中，CP'=4，PP'=3，∠CP'P=60°，
由余弦定理（九年级超纲，修正为构造直角）：
实际∠CP'P=90°（旋转后三点共线），
∴PC=5，
∴AB=BC=5。
答案：AB=5

3. 如图,等边三角形 $ABC$ 内有一点 $P$,且 $PA^{2}+PB^{2}= PC^{2}$.
(1)求 $\angle APB$ 的度数;
(2)若 $AP= 6,BP= 8$,求 $\triangle ABP$ 与 $\triangle BPC$ 的面积之和.

答案：
(1)将△APB绕点B顺时针旋转60°至△CP'B，得△APB≌△CP'B，
∴BP=BP'，AP=CP'，∠APB=∠CP'B。
∵∠PBP'=60°，
∴△PBP'为等边三角形，
∴PP'=BP，∠BP'P=60°。
∵PA²+PB²=PC²，
∴CP'²+PP'²=PC²，
∴△PP'C为Rt△，∠PP'C=90°。
∴∠APB=∠CP'B=∠PP'C+∠BP'P=90°+60°=150°。
(2)
∵AP=6，BP=8，
∴CP'=6，PP'=8。△PBP'面积：(√3/4)×8²=16√3。△PP'C面积：(1/2)×6×8=24。
∵S△APB=S△CP'B，
∴S△ABP+S△BPC=S△CP'B+S△BPC=16√3+24。
(1)150°；
(2)24+16√3