《2025年名校作业九年级数学上册人教版湖北专版》

4. 如图1是一个边长为44 cm的正方形硬纸板,在四个顶点处分别剪掉一个小正方形,折成一个如图2所示的长方体无盖纸盒,则长方体无盖纸盒的侧面积的最大值为______$cm^2$.

968

答案： 设剪掉的小正方形边长为$x$ cm，其中$0 ＜ x ＜ 22$。
折成的长方体纸盒高为$x$ cm，底面边长为$(44 - 2x)$ cm。
侧面积$S$为四个侧面面积之和，每个侧面面积为$(44 - 2x)x$，故：
$S = 4x(44 - 2x)$
化简得：
$S = -8x^2 + 176x$
此为二次函数，$a = -8 ＜ 0$，开口向下，当$x = -\frac{b}{2a} = -\frac{176}{2×(-8)} = 11$时，$S$取最大值。
将$x = 11$代入得：
$S_{max} = -8×11^2 + 176×11 = 968$
968

5. 如图是一个矩形窗框,上面的部分是两个小正方形.若制作窗框的材料总长为6 m,则窗户透光面积的最大值是$\frac{9}{7}$$m^2$.

答案： $\frac{9}{7}$

6. 如图,在正方形ABCD中,AB= 4,P为对角线BD上一动点,F为射线AD上一点.若AP= PF,则△APF面积的最大值为4.

答案： 4

7.【教材P52习题T7变式】如图,正方形ABCD是某公园健身广场的示意图,公园管理处想在其四个角的三角形区域内种植草皮(阴影部分),剩余部分安装健身器材作为市民健身活动场所(四边形EFGH),其中AB= 100米,且AE= AH= CF= CG,请问当AE的长度为多少时,市民健身活动场所的面积达到最大?

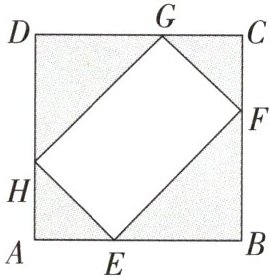
答案： 当AE的长度为50米时，市民健身活动场所的面积达到最大。

8. 在美化校园活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用26 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设BC= x m.
(1)若矩形花园ABCD的面积为165 $m^2$,求x的值;
(2)若在点P处有一棵树,树中心P与墙CD,AD的距离分别是13 m和6 m,要将这棵树围在花园内(考虑到树以后的生长,用篱笆围矩形花园ABCD时,需将以点P为圆心,1 m为半径的圆形区域围在花园内),求矩形花园ABCD的面积S的最大值.

答案：
(1) $ x = 11 $ 或 $ 15 $；
(2) $ 168 \, m^2 $