《2025年名校作业九年级数学上册人教版湖北专版》

3.如图,抛物线$y= -x^{2}+bx+c$与x轴交于A(-5,0),B两点,与y轴交于点C(0,5).
(1)求该抛物线的解析式.
(2)将原抛物线向左平移4个单位长度得到的新抛物线与原抛物线相交于点M,点N为原抛物线对称轴上的一点,在平面内是否存在点H,使以A,M,N,H为顶点的四边形是矩形? 若存在,求出点H的坐标;若不存在,请说明理由.

答案：
(1) 将点$A(-5,0)$、$C(0,5)$代入$y=-x^2+bx+c$，得：
$\begin{cases} 0=-(-5)^2 + b(-5) + c \\ 5 = c \end{cases}$
解得$c=5$，代入第一个方程：$0=-25 -5b +5\Rightarrow b=-4$。
故抛物线解析式为$y=-x^2 -4x +5$。
(2) 原抛物线$y=-(x+2)^2 +9$，向左平移4个单位得新抛物线$y=-(x+6)^2 +9$。
联立$\begin{cases} y=-x^2 -4x +5 \\ y=-x^2 -12x -27 \end{cases}$，解得$x=-4$，$y=5$，即$M(-4,5)$。
原抛物线对称轴为$x=-2$，设$N(-2,n)$。
情况1：以$AN$、$MN$为邻边的矩形
由$AN \perp MN$，$\overrightarrow{AN}=(3,n)$，$\overrightarrow{MN}=(2,n-5)$，
$\overrightarrow{AN} \cdot \overrightarrow{MN}=0\Rightarrow 3×2 + n(n-5)=0\Rightarrow n^2 -5n +6=0$，
解得$n=2$或$n=3$。
$n=2$时：$H=A+M-N=(-5,0)+(-4,5)-(-2,2)=(-7,3)$；
$n=3$时：$H=A+M-N=(-5,0)+(-4,5)-(-2,3)=(-7,2)$。
情况2：以$AM$、$AN$为邻边的矩形
由$AM \perp AN$，$\overrightarrow{AM}=(1,5)$，$\overrightarrow{AN}=(3,n)$，
$\overrightarrow{AM} \cdot \overrightarrow{AN}=0\Rightarrow 1×3 +5n=0\Rightarrow n=-\frac{3}{5}$。
$H=M+N-A=(-4,5)+(-2,-\frac{3}{5})-(-5,0)=(-1,\frac{22}{5})$。
情况3：以$AM$、$MN$为邻边的矩形
由$AM \perp MN$，$\overrightarrow{AM}=(1,5)$，$\overrightarrow{MN}=(2,n-5)$，
$\overrightarrow{AM} \cdot \overrightarrow{MN}=0\Rightarrow 1×2 +5(n-5)=0\Rightarrow n=\frac{23}{5}$。
$H=A+N-M=(-5,0)+(-2,\frac{23}{5})-(-4,5)=(-3,-\frac{2}{5})$。
综上，点$H$的坐标为$(-7,3)$、$(-7,2)$、$(-1,\frac{22}{5})$、$(-3,-\frac{2}{5})$。
答案
(1) $y=-x^2 -4x +5$
(2) 存在，$H$的坐标为$(-7,2)$、$(-7,3)$、$(-1,\frac{22}{5})$、$(-3,-\frac{2}{5})$。

4.如图,抛物线$y= ax^{2}+bx+c$与x轴交于A(4,0),C(-2,0)两点,与y轴交于点B(0,-4),点F(2,-4)是抛物线上的点,连接FA.
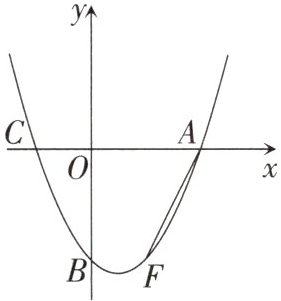
(1)抛物线的解析式为______$y = \frac{1}{2}x^2 - x - 4$.
(2)点Q是第四象限内的一点,点M是平面内一点,是否存在点Q,M,使以A,F,Q,M为顶点的四边形是正方形? 若存在,求出点Q的坐标;若不存在,请说明理由.存在，Q的坐标为$(1, -1)$，$(5, -3)$，$(6, -6)$，$(8, -2)$

答案：
(1) 设抛物线解析式为 $ y = a(x - 4)(x + 2) $，将点 $ B(0, -4) $ 代入得：
$ -4 = a(0 - 4)(0 + 2) $，即 $ -4 = -8a $，解得 $ a = \frac{1}{2} $。
故抛物线解析式为 $ y = \frac{1}{2}(x - 4)(x + 2) = \frac{1}{2}x^2 - x - 4 $。
(2) 存在。
已知 $ A(4, 0) $，$ F(2, -4) $，$ AF = \sqrt{(4 - 2)^2 + (0 + 4)^2} = 2\sqrt{5} $，$ k_{AF} = 2 $，其垂线斜率为 $ -\frac{1}{2} $。
情况1：$ AF $ 为边
过 $ F $ 作 $ AF $ 垂线，设 $ Q(x, y) $，直线方程 $ y = -\frac{1}{2}x - 3 $。由 $ FQ = 2\sqrt{5} $ 得 $ Q(6, -6) $（第四象限）。
过 $ A $ 作 $ AF $ 垂线，直线方程 $ y = -\frac{1}{2}x + 2 $。由 $ AQ = 2\sqrt{5} $ 得 $ Q(8, -2) $（第四象限）。
情况2：$ AF $ 为对角线
中点 $ (3, -2) $，设 $ Q(x, y) $，直线 $ QM $ 斜率 $ -\frac{1}{2} $。由对角线长 $ 2\sqrt{5} $ 得 $ Q(1, -1) $ 和 $ Q(5, -3) $（均在第四象限）。
综上，$ Q $ 的坐标为 $ (1, -1) $，$ (5, -3) $，$ (6, -6) $，$ (8, -2) $。
(1) $ y = \frac{1}{2}x^2 - x - 4 $
(2) 存在，$ Q $ 的坐标为 $ (1, -1) $，$ (5, -3) $，$ (6, -6) $，$ (8, -2) $