第113页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
7. 分别将一把直尺,一块含$60^\circ$角的直角三角尺和一个光盘按如图所示的方式摆放,点A为直角三角尺的斜边与直尺的交点,点B为光盘与直尺的切点.若AB= 3,则光盘的半径为______
$3\sqrt{3}$
.
答案:
设光盘圆心为O,半径为r,连接OB,因光盘与直尺相切于B,故OB⊥直尺,OB=r。
设三角尺60°角顶点为A,斜边与直尺交于A,另一直角边(或斜边)与光盘相切,圆心O到该边距离为r。
由AB=3,过O作该边垂线,垂足为C,则OC=r。
在Rt△OAB中,∠OAB=60°,OB=r,AB=3,tan60°=OB/AB,即√3=r/3,解得r=3√3。
答案:$3\sqrt{3}$
设三角尺60°角顶点为A,斜边与直尺交于A,另一直角边(或斜边)与光盘相切,圆心O到该边距离为r。
由AB=3,过O作该边垂线,垂足为C,则OC=r。
在Rt△OAB中,∠OAB=60°,OB=r,AB=3,tan60°=OB/AB,即√3=r/3,解得r=3√3。
答案:$3\sqrt{3}$
8. 如图,将Rt$\triangle ABC平移到\triangle A'B'C'$的位置,使得点$C'与\triangle ABC$的内心重合.已知$\angle C= 90^\circ$,$AC= 4$,$BC= 3$,则阴影部分的周长为______
5
.
答案:
解答过程:
1. 计算Rt△ABC的斜边及内切圆半径
在Rt△ABC中,∠C=90°,AC=4,BC=3,由勾股定理得斜边AB=√(AC²+BC²)=√(4²+3²)=5。
内切圆半径r=(AC+BC-AB)/2=(4+3-5)/2=1。
2. 确定内心坐标及平移性质
△ABC的内心到三边距离均为r=1,以C为原点建立坐标系,内心坐标为(1,1)(即C'的位置)。平移后A'C'//AC,B'C'//BC,A'B'//AB。
3. 求阴影部分顶点坐标及边长
A'C'(竖直线x=1)与AB交于D(1, 8/3),B'C'(水平线y=1)与AB交于E(9/4,1),C'(1,1)构成阴影△C'DE。
C'D=8/3 -1=5/3,
EC'=9/4 -1=5/4,
DE=√[(9/4 -1)²+(1 -8/3)²]=25/12。
4. 计算阴影部分周长
周长=C'D+DE+EC'=5/3 +25/12 +5/4=5。
最终结论:5
1. 计算Rt△ABC的斜边及内切圆半径
在Rt△ABC中,∠C=90°,AC=4,BC=3,由勾股定理得斜边AB=√(AC²+BC²)=√(4²+3²)=5。
内切圆半径r=(AC+BC-AB)/2=(4+3-5)/2=1。
2. 确定内心坐标及平移性质
△ABC的内心到三边距离均为r=1,以C为原点建立坐标系,内心坐标为(1,1)(即C'的位置)。平移后A'C'//AC,B'C'//BC,A'B'//AB。
3. 求阴影部分顶点坐标及边长
A'C'(竖直线x=1)与AB交于D(1, 8/3),B'C'(水平线y=1)与AB交于E(9/4,1),C'(1,1)构成阴影△C'DE。
C'D=8/3 -1=5/3,
EC'=9/4 -1=5/4,
DE=√[(9/4 -1)²+(1 -8/3)²]=25/12。
4. 计算阴影部分周长
周长=C'D+DE+EC'=5/3 +25/12 +5/4=5。
最终结论:5
9. 如图是由边长相等的小正方形组成的网格,每个小正方形的顶点叫做格点,点O,E均为格点,过点E作$\odot O$的切线EM,EN,切点分别为M,N(点M在点N的左侧),仅用无刻度的直尺在给定的网格中完成作图(保留作图痕迹,不写作法).


答案:
(以下为作图痕迹描述,实际作答需在图中完成)
1. 连接格点O与格点E。
2. 在⊙O上找出两个格点M、N(M在N左侧),使得OM⊥EM,ON⊥EN。
3. 连接EM、EN,即为所求切线。
(注:实际作图时,通过网格格点连线构造直角,确定切点M、N后连接E与M、E与N。)
1. 连接格点O与格点E。
2. 在⊙O上找出两个格点M、N(M在N左侧),使得OM⊥EM,ON⊥EN。
3. 连接EM、EN,即为所求切线。
(注:实际作图时,通过网格格点连线构造直角,确定切点M、N后连接E与M、E与N。)
10. 如图,点E是$\triangle ABC$的内心,AE的延长线与$\triangle ABC$的外接圆相交于点D,连接BE,CE,BD,CD.
(1)若$\angle CBD= 34^\circ$,求$\angle BEC$的度数.
(2)求证:$DE= DB$.

(1)若$\angle CBD= 34^\circ$,求$\angle BEC$的度数.
(2)求证:$DE= DB$.

答案:
(1)
∵∠CBD=34°,∠CBD与∠CAD所对弧均为CD,
∴∠CAD=∠CBD=34°。
∵E是△ABC内心,AE平分∠BAC,
∴∠BAC=2∠CAD=68°。
在△ABC中,∠ABC+∠ACB=180°-∠BAC=112°。
∵BE、CE分别平分∠ABC、∠ACB,
∴∠EBC=1/2∠ABC,∠ECB=1/2∠ACB。
∴∠EBC+∠ECB=1/2(∠ABC+∠ACB)=56°。
∴∠BEC=180°-(∠EBC+∠ECB)=124°。
(2) 证明:
∵∠DBE=∠DBC+∠CBE,∠DBC=∠CAD(同弧CD所对圆周角),E为内心,CE平分∠ACB,BE平分∠ABC,
∴∠CBE=1/2∠ABC,∠CAD=1/2∠BAC(AE平分∠BAC)。
∴∠DBE=1/2∠BAC+1/2∠ABC。
∵∠DEB是△ABE的外角,
∴∠DEB=∠EAB+∠EBA。
∵AE平分∠BAC,BE平分∠ABC,
∴∠EAB=1/2∠BAC,∠EBA=1/2∠ABC。
∴∠DEB=1/2∠BAC+1/2∠ABC。
∴∠DBE=∠DEB,
∴DE=DB。
(1)
∵∠CBD=34°,∠CBD与∠CAD所对弧均为CD,
∴∠CAD=∠CBD=34°。
∵E是△ABC内心,AE平分∠BAC,
∴∠BAC=2∠CAD=68°。
在△ABC中,∠ABC+∠ACB=180°-∠BAC=112°。
∵BE、CE分别平分∠ABC、∠ACB,
∴∠EBC=1/2∠ABC,∠ECB=1/2∠ACB。
∴∠EBC+∠ECB=1/2(∠ABC+∠ACB)=56°。
∴∠BEC=180°-(∠EBC+∠ECB)=124°。
(2) 证明:
∵∠DBE=∠DBC+∠CBE,∠DBC=∠CAD(同弧CD所对圆周角),E为内心,CE平分∠ACB,BE平分∠ABC,
∴∠CBE=1/2∠ABC,∠CAD=1/2∠BAC(AE平分∠BAC)。
∴∠DBE=1/2∠BAC+1/2∠ABC。
∵∠DEB是△ABE的外角,
∴∠DEB=∠EAB+∠EBA。
∵AE平分∠BAC,BE平分∠ABC,
∴∠EAB=1/2∠BAC,∠EBA=1/2∠ABC。
∴∠DEB=1/2∠BAC+1/2∠ABC。
∴∠DBE=∠DEB,
∴DE=DB。
11. 如图1,AB是$\odot O$的直径,AD与$\odot O$相切于点A,DE与$\odot O$相切于点E,C为DE的延长线上一点,且$CE= CB$.
(1)求证:BC为$\odot O$的切线.
(2)如图2,连接AE并延长,交BC的延长线于点G.若$\odot O的半径为\sqrt{5}$,$AD= 2$,求线段CE和AG的长.
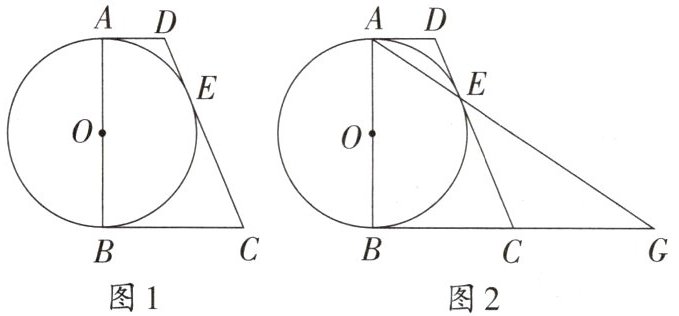
(1)求证:BC为$\odot O$的切线.
(2)如图2,连接AE并延长,交BC的延长线于点G.若$\odot O的半径为\sqrt{5}$,$AD= 2$,求线段CE和AG的长.

答案:
(1)连接OE、OC。
∵AD、DE是⊙O的切线,
∴AD=DE,∠OAD=∠OED=90°。
∵CE=CB,OE=OB(半径),OC=OC(公共边),
∴△OEC≌△OBC(SSS)。
∴∠OBC=∠OEC=90°。
∵OB是半径,
∴BC为⊙O的切线。
(2)设CE=CB=x,⊙O半径为√5,
∴AB=2√5,AD=DE=2(切线长定理),则CD=DE+CE=2+x。
以A为原点,AB为x轴,AD为y轴建立坐标系:A(0,0),B(2√5,0),D(0,2),O(√5,0)。
设E(x,y),由OE⊥DE及OE=√5,DE=2,得:
√(x²+(y-2)²)=2,(x-√5)²+y²=5,解得E(8√5/9,20/9)。
DE直线方程:y=(√5/20)x+2。
∵C在DE上且CE=CB,设C(m,n),则n=(√5/20)m+2,且(m-2√5)²+n²=(m-8√5/9)²+(n-20/9)²,解得m=2√5,n=5/2。
∴CE=√[(2√5-8√5/9)²+(5/2-20/9)²]=5/2。
直线AE:过A(0,0),E(8√5/9,20/9),斜率k=√5/2,方程y=(√5/2)x。
BC为x=2√5,与AE交于G(2√5,5)。
AG=√[(2√5)²+5²]=3√5。
(1)证明完毕;
(2)CE=5/2,AG=3√5。
(1)连接OE、OC。
∵AD、DE是⊙O的切线,
∴AD=DE,∠OAD=∠OED=90°。
∵CE=CB,OE=OB(半径),OC=OC(公共边),
∴△OEC≌△OBC(SSS)。
∴∠OBC=∠OEC=90°。
∵OB是半径,
∴BC为⊙O的切线。
(2)设CE=CB=x,⊙O半径为√5,
∴AB=2√5,AD=DE=2(切线长定理),则CD=DE+CE=2+x。
以A为原点,AB为x轴,AD为y轴建立坐标系:A(0,0),B(2√5,0),D(0,2),O(√5,0)。
设E(x,y),由OE⊥DE及OE=√5,DE=2,得:
√(x²+(y-2)²)=2,(x-√5)²+y²=5,解得E(8√5/9,20/9)。
DE直线方程:y=(√5/20)x+2。
∵C在DE上且CE=CB,设C(m,n),则n=(√5/20)m+2,且(m-2√5)²+n²=(m-8√5/9)²+(n-20/9)²,解得m=2√5,n=5/2。
∴CE=√[(2√5-8√5/9)²+(5/2-20/9)²]=5/2。
直线AE:过A(0,0),E(8√5/9,20/9),斜率k=√5/2,方程y=(√5/2)x。
BC为x=2√5,与AE交于G(2√5,5)。
AG=√[(2√5)²+5²]=3√5。
(1)证明完毕;
(2)CE=5/2,AG=3√5。
查看更多完整答案,请扫码查看


