第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
利用相似三角形测高
测量原理:
测量旗杆(或路灯杆)高度的三种方法:
(1) 利用阳光下的影子;
(2) 利用标杆;
(3) 利用镜子的反射.
测量原理:
相似三角形对应边成比例
.测量旗杆(或路灯杆)高度的三种方法:
(1) 利用阳光下的影子;
(2) 利用标杆;
(3) 利用镜子的反射.
答案:
相似三角形对应边成比例
1. 一根 $1.5$ m 长的标杆直立在水平地面上,它在阳光下的影长为 $2.1$ m,此时一棵水杉树的影长为 $10.5$ m,这棵水杉树高为(
A.$7.5$ m
B.$8$ m
C.$14.7$ m
D.$15.75$ m
A
).A.$7.5$ m
B.$8$ m
C.$14.7$ m
D.$15.75$ m
答案:
A
2. 如图所示的是小明设计用手电筒来测量某古城墙高度的示意图,点 $P$ 处放一水平的平面镜,光线从点 $A$ 出发经平面镜反射后刚好射到古城墙 $CD$ 的顶端 $C$ 处. 已知 $AB \perp BD$,$CD \perp BD$,且测得 $AB = 1.2$ m,$BP = 1.8$ m,$PD = 12$ m,那么该古城墙的高度是(
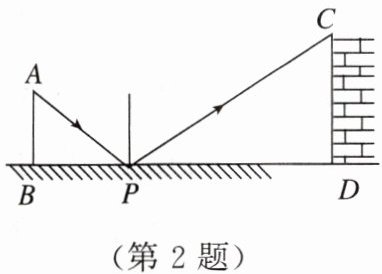
A.$6$ m
B.$8$ m
C.$18$ m
D.$24$ m
B
).
A.$6$ m
B.$8$ m
C.$18$ m
D.$24$ m
答案:
B
3. 为测量广场上旗杆 $AB$ 的高度,设计的测量方案如图所示:标杆高度 $CD = 3$ m,标杆与旗杆的水平距离 $BD = 15$ m,人的眼睛与地面的高度 $EF = 1.6$ m,人与标杆 $CD$ 的水平距离 $DF = 2$ m,$E$,$C$,$A$ 三点共线,则旗杆 $AB$ 的高度为(

A.$15$ m
B.$14.5$ m
C.$13.5$ m
D.$13$ m
C
).
A.$15$ m
B.$14.5$ m
C.$13.5$ m
D.$13$ m
答案:
C
4. 如图,身高为 $1.7$ m 的小明 $AB$ 站在河的一岸,利用树的倒影去测量河对岸一棵树 $CD$ 的高度,$CD$ 在水中的倒影为 $C'D$,$A$,$E$,$C'$ 在一条直线上. 已知河 $BD$ 的宽度为 $12$ m,$BE = 3$ m,则树 $CD$ 的高为

5.1m
.
答案:
5.1m
5. 如图,利用标杆 $BE$ 测量建筑物的高度,标杆 $BE$ 高 $1.5$ m,测得 $AB = 2$ m,$BC = 14$ m,则楼高 $CD$ 为
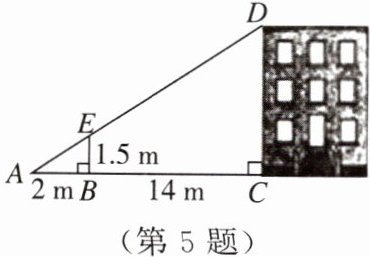
12
m.
答案:
12
查看更多完整答案,请扫码查看


