《2025年配套综合练习甘肃九年级数学上册北师大版》

13. 有$x$支球队参加篮球比赛,每两队之间都比赛一场,共比赛了$45$场,则下列方程符合题意的是(A)。
A.$\frac{1}{2}x(x - 1)= 45$
B.$\frac{1}{2}x(x + 1)= 45$
C.$x(x - 1)= 45$
D.$x(x + 1)= 45$

答案： A

1. 能够使方程左、右两边相等的未知数的值叫做方程的解,只含有一个未知数的方程的解也叫方程的根。

答案： 未知数的值 一

2. 对于实际问题列出一元二次方程,先确定解的大致范围,再通过具体计算,两边夹逼,逐渐找到近似解,这就是估算一元二次方程近似解的方法,这种数学思想叫做夹逼思想,夹逼思想是求一元二次方程近似解的重要思想。

答案： 夹逼 近似 夹逼思想 夹逼

1. 已知关于 $ x $ 的方程 $ x^{2}-px + q = 0 $ 有一根为 $ 0 $,则 $ q $ 的值为(A)。
A.$ 0 $
B.$ 1 $
C.$ 2 $
D.无法求解

答案： A

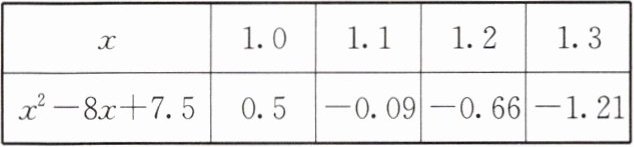
2. 根据下表确定方程 $ x^{2}-8x + 7.5 = 0 $ 的解的范围是1.0＜x＜1.1。

答案： 1.0＜x＜1.1

3. 若 $ x = 1 $ 是关于 $ x $ 的方程 $ x^{2}-3kx - 10 = 0 $ 的一个根,则 $ k = $-3。

答案： -3

4. 先填表,再填空：

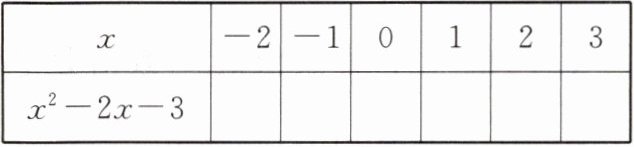
根据上表可知方程 $ x^{2}-2x - 3 = 0 $ 的根是x₁=-1,x₂=3。

答案： 5 0 -3 -4 -3 0 x₁=-1,x₂=3

5. 判断下列方程后面括号里的数是不是方程的解。
(1) $ x^{2}+5x - 6 = 0 $,$ (1,-6) $；
(2) $ x^{2}-2\sqrt{3}x + 3 = 0 $,$ (\sqrt{3},1) $；
(3) $ (2x - 1)^{2}= 3 $,$ (\frac{1 + \sqrt{3}}{2},\frac{1 - \sqrt{3}}{2}) $。

答案： 解:
(1)1,-6均为方程的解；
(2)$\sqrt{3}$是方程的解,1不是方程的解；
(3)$\frac{1\pm\sqrt{3}}{2}$均为方程的解.