第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
11. 在研究相似问题时,甲、乙同学的观点如下.
甲:将边长为 3,4,5 的三角形按图①的方式向外扩张,得到新三角形,它们的对应边间距为 1,则新三角形与原三角形相似.
乙:将邻边为 3 和 5 的矩形按图②的方式向外扩张,得到新的矩形,它们的对应边间距均为 1,则新矩形与原矩形不相似.
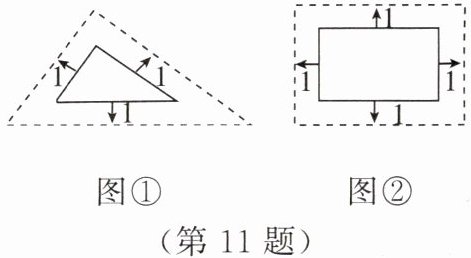
对于两人的观点,下列说法正确的是(
A.两人都对
B.两人都不对
C.甲对、乙不对
D.甲不对、乙对
甲:将边长为 3,4,5 的三角形按图①的方式向外扩张,得到新三角形,它们的对应边间距为 1,则新三角形与原三角形相似.
乙:将邻边为 3 和 5 的矩形按图②的方式向外扩张,得到新的矩形,它们的对应边间距均为 1,则新矩形与原矩形不相似.

对于两人的观点,下列说法正确的是(
A
).A.两人都对
B.两人都不对
C.甲对、乙不对
D.甲不对、乙对
答案:
11.A
| 一般地,点 $ C $ 把线段 $ AB $ 分成两条线段 $ AC $ 和 $ BC $ ($ AC>BC $),如果
$\frac{AC}{AB}=\frac{BC}{AC}$
,那么称线段 $ AB $ 被点 $ C $ 黄金分割
,点 $ C $ 叫做线段 $ AB $ 的 黄金分割点
,$ AC $ 与 $ AB $ 的比叫做 黄金比
,等于 $\frac{\sqrt{5}-1}{2}$
,约为 0.618
.
答案:
$\frac{AC}{AB}=\frac{BC}{AC}$ 黄金分割 黄金分割点 黄金比 $\frac{\sqrt{5}-1}{2}$ 0.618
1. 如图,点 $ C $ 把线段 $ AB $ 分成两条线段 $ AC $ 和 $ BC $,如果 $ \frac{AC}{AB}= \frac{BC}{AC} $,那么下列说法错误的是(
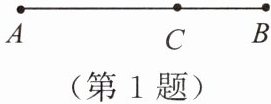
A.线段 $ AB $ 被点 $ C $ 黄金分割
B.点 $ C $ 叫做线段 $ AB $ 的黄金分割点
C.$ AB $ 与 $ AC $ 的比叫做黄金比
D.$ AC $ 与 $ AB $ 的比叫做黄金比
C
).
A.线段 $ AB $ 被点 $ C $ 黄金分割
B.点 $ C $ 叫做线段 $ AB $ 的黄金分割点
C.$ AB $ 与 $ AC $ 的比叫做黄金比
D.$ AC $ 与 $ AB $ 的比叫做黄金比
答案:
C
2. 已知点 $ P $ 是线段 $ AB $ 的黄金分割点,$ AP>PB $,则下列等式不成立的是(
A.$ AP^{2}= PB\cdot AB $
B.$ AP= \frac{\sqrt{5}-1}{2}AB $
C.$ PB= \frac{3-\sqrt{5}}{2}AB $
D.$ BP^{2}= AP\cdot AB $
D
).A.$ AP^{2}= PB\cdot AB $
B.$ AP= \frac{\sqrt{5}-1}{2}AB $
C.$ PB= \frac{3-\sqrt{5}}{2}AB $
D.$ BP^{2}= AP\cdot AB $
答案:
D
查看更多完整答案,请扫码查看


