《2025年配套综合练习甘肃九年级数学上册北师大版》

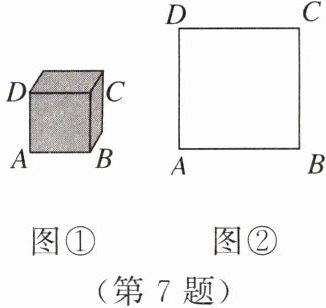
7. 如图①,李叔叔想要检测雕塑底座正面四边形 $ABCD$ 是不是正方形,但他随身只带了有刻度的卷尺. 请你设计一种方案,帮助李叔叔检测四边形 $ABCD$ 是不是正方形. (图②供设计备用)

答案： 解:方案不唯一,例如
(1)用卷尺分别比较AB,CD,AD,BC的长度,当AB=CD=AD=BC时,四边形ABCD为菱形,否则四边形ABCD不是菱形,从而不是正方形.
(2)当四边形ABCD是菱形时,用卷尺比较对角线AC和BD的长度.当AC=BD时,四边形ABCD是正方形,否则四边形ABCD不是正方形.

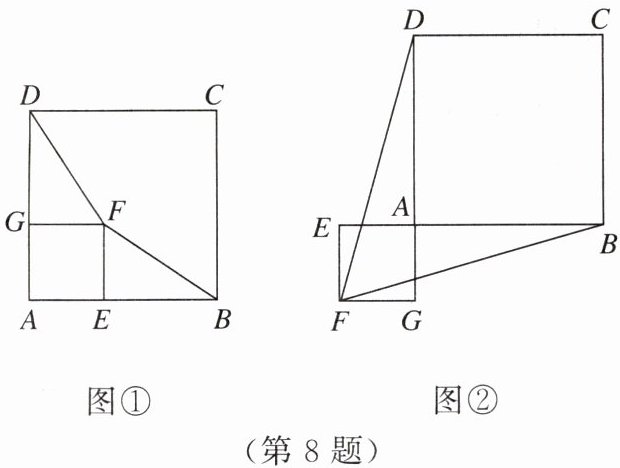
8. 正方形 $ABCD$ 和正方形 $AEFG$ 有公共顶点 $A$.
(1)如图①,若点 $E$,$G$ 分别在 $AB$,$AD$ 上,求证：$DF = BF$.
(2)将(1)中正方形 $AEFG$ 绕点 $A$ 按顺时针方向旋转 $180^{\circ}$,使得点 $E$,$G$ 分别在 $BA$,$DA$ 的延长线上,连接 $DF$,$BF$,如图②,判断 $DF$ 与 $BF$ 是否还相等,请说明理由.

答案：
(1)证明:
∵四边形ABCD和四边形AEFG均为正方形,
∴AG=AE,AD=AB,GF=EF,∠DGF=∠BEF=90°,
∴DG=BE.
在△DGF和△BEF中,{DG=BE,∠DGF=∠BEF,GF=EF,
∴△DGF≌△BEF(SAS),
∴DF=BF.
(2)解:DF=BF.
理由如下:方法1:连接AF(图略).
∵四边形ABCD和四边形AEFG均为正方形,
∴AD=AB,∠FAG=∠FAE=45°,∠BAG=∠DAE=90°,
∴∠BAF=∠DAF=135°.
在△DAF和△BAF中,{AD=AB,∠DAF=∠BAF,AF=AF,
∴△DAF≌△BAF(SAS),
∴DF=BF.
方法2:证明△BEF≌△DGF(SAS)也可以.